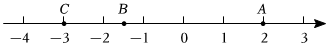（1）探索材料1（填空）：
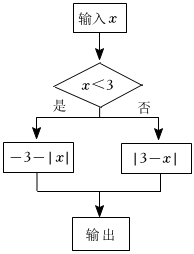
數軸上表示數m和數n的兩點之間的距離等于|m-n|．例如數軸上表示數3和6的兩點距離為|3-6|=3；數軸上表示數3和-2的兩點距離為|3-（-2）|=

5

5

；代數式|x-4|的意義可理解為數軸上表示數

x

x

和數

4

4

這兩點的距離．
（2）探索材料2：|x-2|=5的意義可理解為數軸上表示數x的點到數2的點的距離為5，由于數軸上數-3和數7到數2的距離為5，故使|x-2|=5成立的x的值為-3或7．求使|x-3|=5成立的x的值．
（3）探索材料3：代數式|x+3|+|x-2|的意義可理解為數軸上表示數x的點到數-3的點的距離和數x的點到數2的點的距離之和，不妨記數軸上數2為點A，數x為點B，數-3為點C．若要求|x+3|+|x-2|的最小值，即求BC+BA的最小值．結合數軸可知，當點B在A點和C點之間時，BC+BA最小，最小值為AC=2-（-3）=5．綜上，|x+3|+|x-2|的最小值為5．
①求代數式|x+2|+|x-4|的最小值；
②求代數式|x+5|+|x+1|+|x-2|的最小值．