[學習心得]
（1）寧寧在學習完“圓”這一章內容后，感覺到一些幾何問題如果添加輔助圓，運用圓的知識解決，可以使問題變得非常容易，
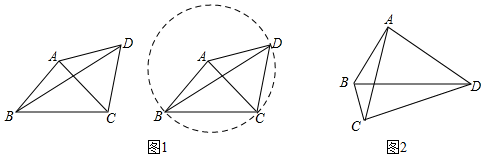
例如：如圖1，在△ABC中，AB=AC，∠BAC=90°．D是△ABC外一點，且AD=AC，求∠BDC的度數．若以點A為圓心，AB長為半徑作輔助圓⊙A，則C，D兩點必在⊙A上，∠BAC是⊙A的圓心角，∠BDC是⊙A的圓周角，則∠BDC=4545°；
[初步運用]
（2）如圖2，在四邊形ABCD中，∠BAD=∠BCD=90°，∠BDC=26°，求∠BAC的度數；
[方法遷移]
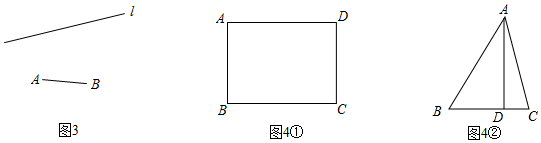
（3）如圖3，已知線段AB和直線l,用直尺和圓規在l上作出所有的點P，使得∠APB=30°（不寫作法，保留作圖痕跡）；
[問題拓展]
（4）①如圖4①，已知矩形ABCD，AB=2，BC=m,點M為邊CD上的一點．
若滿足∠AMB=45°的點M恰好有兩個，則m的取值范圍為 2≤m＜2+12≤m＜2+1．
②如圖4②，在△ABC中，∠BAC=45°，AD是BC邊上的高，且BD=6，CD=2，求AD的長，
2
2
【考點】圓的綜合題．
【答案】45；2≤m＜+1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：407引用：1難度：0.1
相似題
-
1．請僅用無刻度的直尺完成下列畫圖，不寫畫法，保留畫圖痕跡．
（1）如圖1，△ABC的外接圓的圓心是點O，D是弧BC的中點，畫一條弦AE把△ABC分成面積相等的兩部分；
（2）如圖2，△ABC是⊙O的內接三角形，且AB=AC，過點B畫弦BD∥AO；
（3）如圖3，△ABC是⊙O的內接三角形，弦AD∥BC，畫∠BAC的平分線交BC于點E．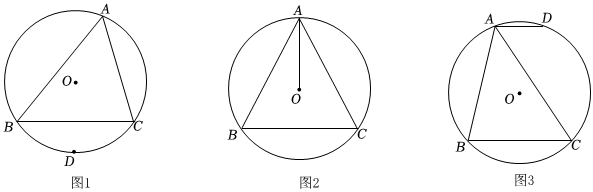
發布：2025/5/22 8:0:2組卷：187引用：1難度：0.1 -
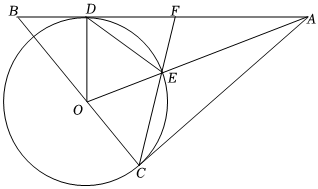2．如圖，在△ABC的邊BC上取一點O，以O為圓心，OC為半徑畫⊙O，⊙O與邊AB相切于點D，AC=AD，連接OA交⊙O于點E，連接CE，并延長交線段AB于點F．
（1）求證：AC是⊙O的切線；
（2）若AB=10，tanB=，求⊙O的半徑；43
（3）若F是AB的中點，求證：CE+BD=AF．發布：2025/5/22 8:0:2組卷：591引用：3難度：0.3 -
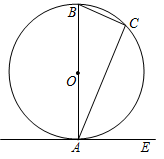3．如圖，已知AB是⊙O的直徑，AB=10，點C在⊙O上，點E在⊙O外．
（1）動手操作：作∠ACB的角平分線CD，與圓交于點D（要求：尺規作圖，不寫作法，保留作圖痕跡）
（2）綜合運用，在你所作的圖中．
①連接AD，求AD的長．
②若∠EAC=∠D，求證：AE是⊙O的切線．發布：2025/5/22 8:0:2組卷：306引用：3難度：0.4