 【閱讀材料】
【閱讀材料】
配方法不僅可以解一元二次方程,還可以用來求“最值”問題.
例如:求代數式2m2+4m+5的最值.
解:因為2m2+4m+5
=(2m2+4m)+5(分離常數項)
=2(m2+2m)+5(提二次項系數)
=2(m2+2m+1-1)+5 =2[(m+1)2-1]+5 =2(m+1)2+3
(配方)
所以當m=-1時,代數式2m2+4m+5取得最小值3.
再如:求代數式-2m2+6m的最值.
解:因為-2m2+6m
=-2(m2-3m)
=-2(m2-3m+94-94)
=-2(m-32)2+92
所以當m=32時,代數式-2m2+6m取得最大值92.
【材料理解】
x=-2-2時,代數式-3(x+2)2-4的最 大大(“大”或“小”)值為 -4-4.
【類比應用】
試判斷關于x的一元二次方程x2-(k-3)x-2k=0實數根的情況,并說明理由.
【遷移應用】
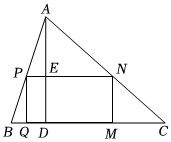
如圖,有一塊銳角三角形余料ABC,它的邊BC=12厘米,高AD=8厘米.現要用它裁出一個矩形工件PQMN,使矩形的一邊在BC上,其余的兩個頂點分別在AB、AC上.
①設PN=x,試用含x的代數式表示矩形工件PQMN的面積S;
②運用“配方法”求S的最大值.
= 2 ( m 2 + 2 m + 1 - 1 ) + 5 |
= 2 [ ( m + 1 ) 2 - 1 ] + 5 |
= 2 ( m + 1 ) 2 + 3 |
-
2
(
m
2
-
3
m
+
9
4
-
9
4
)
-
2
(
m
-
3
2
)
2
+
9
2
m
=
3
2
9
2
【答案】-2;大;-4
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/10/12 5:0:1組卷:375引用:2難度:0.5
相似題
-
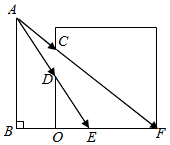 1.如圖,學校平房的窗外有一路燈AB,路燈光能通過窗戶CD照到平房內EF處;經過測量得:窗戶距地面高OD=1.5m,窗戶高度DC=0.8m,OE=1m,OF=3m;求路燈AB的高.發布:2025/6/8 16:30:1組卷:1385引用:5難度:0.7
1.如圖,學校平房的窗外有一路燈AB,路燈光能通過窗戶CD照到平房內EF處;經過測量得:窗戶距地面高OD=1.5m,窗戶高度DC=0.8m,OE=1m,OF=3m;求路燈AB的高.發布:2025/6/8 16:30:1組卷:1385引用:5難度:0.7 -
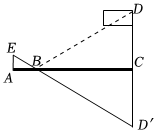 2.雨后初晴,小明在操場上玩耍,從他前面2米遠的一小塊積水處,他看到了旗桿頂端的倒影,如果旗桿底端到積水處的距離為40米,小明的眼部高度是1.5米,那么,旗桿的高度是 米.發布:2025/6/8 16:30:1組卷:10引用:1難度:0.6
2.雨后初晴,小明在操場上玩耍,從他前面2米遠的一小塊積水處,他看到了旗桿頂端的倒影,如果旗桿底端到積水處的距離為40米,小明的眼部高度是1.5米,那么,旗桿的高度是 米.發布:2025/6/8 16:30:1組卷:10引用:1難度:0.6 -
3.小明測得2m高的標桿在太陽光下的影長為1.2m,同時同地又測得一棵樹的影長為1.8m,則這棵樹的高度是m.
發布:2025/6/8 19:30:1組卷:151引用:4難度:0.7


