【問題提出】
數學課上，學習了直角三角形全等的判定方法（即“HL”）后，我們繼續對“兩個直角三角形滿足一條直角邊和周長分別相等”的情形進行研究．
【問題解決】
（1）如圖①，在Rt△ABC和Rt△DEF中，∠B=∠E=90°，AB=DE，△ABC和△DEF的周長相等．求證：△ABC≌△DEF．
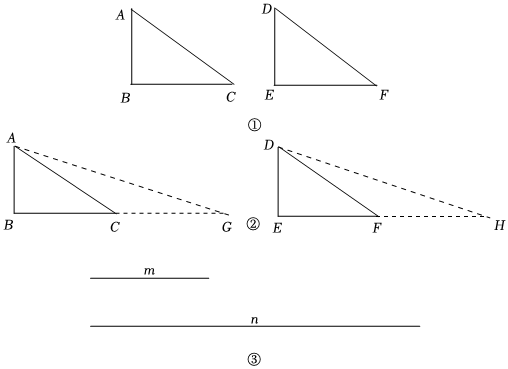
（Ⅰ）根據小紅的思考，請將小紅的解答過程補充完整；
小紅的思考
| 設AB=DE=m,△ABC的周長=△DEF的周長=n,AC=x. 在Rt△ABC中，根據勾股定理，得 m2+（n-m-x）2=x2 m2+（n-m-x）2=x2 ，解得x = 2 m 2 + n 2 - 2 mn 2 n - 2 m 同理可得 DF = 2 m 2 + n 2 - 2 mn 2 n - 2 m 根據 HL HL ，可以知道Rt△ABC≌Rt△DEF． |
小明的思考
| 如圖②，在Rt△ABC和Rt△DEF中，分別延長BC，EF至G，H，使得CG=AC，FH=DF，連接AG，DH． |
（2）如圖③，已知線段m,n.用直尺和圓規求作一個Rt△ABC，使∠B=90°，AB=m,△ABC的周長為n.（保留作圖痕跡，寫出必要的文字說明）
（3）下列命題是真命題的有
A，B，C
A，B，C
．A．斜邊和周長分別相等的兩個直角三角形全等
B．斜邊和面積分別相等的兩個直角三角形全等
C．一個銳角和周長分別相等的兩個直角三角形全等
D．斜邊和斜邊上的中線分別相等的兩個直角三角形全等
【考點】三角形綜合題．
【答案】m2+（n-m-x）2=x2；HL；A，B，C
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：742引用：1難度：0.2
相似題
-
1．某興趣小組探索等腰三角形中線段比值問題，部分探索活動如下：
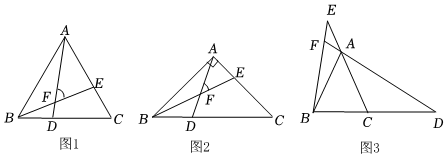
（1）如圖1，在△ABC中，AB=AC，∠ABC=60°，D，E分別是BC，AC邊上的點，∠AFE=∠ABC，則的值為 ．BEAD
（2）如圖2，在△ABC中，AB=AC，∠ABC=45°，D，E分別是BC，AC邊上的點，∠AFE=∠ABC，請你猜想的值，并給出證明；BEAD
（3）如圖3，在△ABC中，AB=AC，，D，E分別是BC，CA邊延長線上的點，∠DFB=∠ABC，請直接寫出cos∠ABC=512的值．BEAD發布：2025/5/26 0:0:1組卷：153引用：1難度：0.4 -
2．在△ABC中，AB=AC，BC=12，E為邊AC的中點，
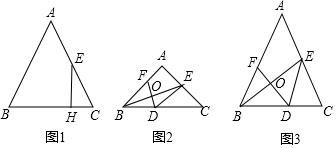
（1）如圖1，過點E作EH⊥BC，垂足為點H，求線段CH的長；
（2）作線段BE的垂直平分線分別交邊BC、BE、AB于點D、O、F．
①如圖2，當∠BAC=90°時，求BD的長；
②如圖3，設tan∠ACB=x,BD=y,求y與x之間的函數表達式和tan∠ACB的最大值．發布：2025/5/26 1:0:1組卷：278引用：2難度：0.1 -
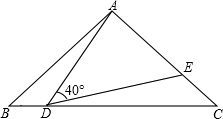3．如圖，在△ABC中，AB=AC=2，∠B=40°，點D在線段BC上運動（D不與B、C重合），連接AD，作∠ADE=40°，DE交線段AC于E．
（1）當∠BDA=115°時，∠BAD=°，∠DEC=°；
（2）當DC等于多少時，△ABD與△DCE全等？請說明理由；
（3）在點D的運動過程中，△ADE的形狀可以是等腰三角形嗎？若可以，請直接寫出∠BDA的度數．若不可以，請說明理由．發布：2025/5/26 2:30:2組卷：976引用：8難度：0.3