根據以下素材，探索完成任務．
| 如何確定隧道的限高？ | ||||
| 素材1 | 從小清家到附近山區(qū)的一條雙行線公路上有一個隧道，在隧道口有一個限高標志（如圖1），表示禁止裝載高度（車頂最高處到地面）超過3.5m的車輛通行．那么這個限高3.5m是如何確定的呢？ |
|
||
| 素材2 | 小清通過實地調查和查閱相關資料，獲得以下信息： ①隧道的橫截面成軸對稱，由一個矩形和一個弓形構成． ②隧道內的總寬度為8m,雙行車道寬度為6m,隧道圓拱內壁最高處距路面5m,矩形的高為2m,車道兩側的人行道寬1m. ③為了保證安全，交通部門要求行駛車輛的頂部（設為平頂）與隧道圓拱內壁在豎直方向上的高度差相差最少0.2m. |
|
||
| 問題解決 | ||||
| 任務1 | 計算半徑 | 求圖1中弓形所在圓的半徑． | ||
| 任務2 | 確定限高 | 如圖2，在安全的條件下，3.5m的限高是如何確定的？請通過計算說明理由．（參考數(shù)據： 301 |
||
| 任務3 | 嘗試設計 | 如果要使高度不超過3.3m,寬為2.5m的貨車能順利通過這個隧道，且不改變隧道內的總寬度（8m）和矩形的高（2m），如何設計隧道的弓形部分（求弓形所在圓的半徑至少為多少米？）（參考數(shù)據： 89 |
||
【考點】圓的綜合題．
【答案】（1）；
（2）見（2）中解析；
（3）4.7．
25
6
（2）見（2）中解析；
（3）4.7．
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網所有，未經書面同意，不得復制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：376引用：1難度：0.1
相似題
-
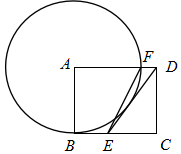1．如圖，在矩形ABCD中，點E是BC邊上一點，且AD=DE，以AB為半徑作⊙A，交AD邊于點F，連接EF．
（1）求證：DE是⊙A的切線；
（2）若AB=2，BE=1，求AD的長；
（3）在（2）的條件下，求tan∠FED．發(fā)布：2025/5/24 17:30:1組卷：161引用：2難度：0.4 -
2．（1）如圖1，⊙A的半徑為2，AB=5，點P為⊙A上任意一點，則BP的最小值為 ．
（2）如圖2，已知矩形ABCD，點E為AB上方一點，連接AE，BE，作EF⊥AB于點F，點P是△BEF的內心，求∠BPE的度數(shù)．
（3）如圖3，在（2）的條件下，連接AP，CP，若矩形的邊長AB=6，BC=4，BE=BA，求此時CP的最小值．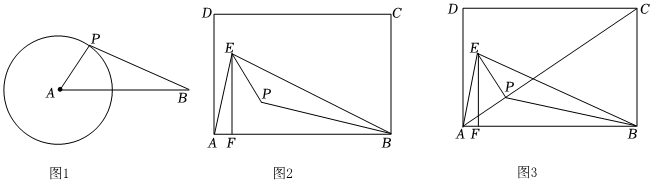
發(fā)布：2025/5/24 16:30:1組卷：1241引用：6難度：0.3 -
3．微探究：如圖①，點P在⊙O上，利用直尺（沒有刻度）和圓規(guī)過點P作⊙O的切線．小明所在的數(shù)學小組經過合作探究，發(fā)現(xiàn)了很多作法，精彩紛呈．
作法一：
①作直徑PA的垂直平分線交⊙O于點B；
②分別以點B、P為圓心，OP為半徑作弧，兩弧交于點C；
③作直線PC．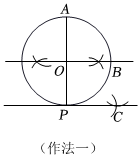
作法二：
①作直徑PA的四等分點B、C；
②以點A為圓心，CA為半徑作弧，交射線PA于點D；
③分別以點A、P為圓心，PD、PC為半徑作弧，兩弧交于點E；
④作直線PE．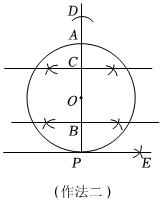
（1）以上作法是否正確？選一個你認為正確的作法予以證明；
（2）在圖①、圖②中用兩種作法作出符合條件的圖形（與以上作法不同）．不寫作法，保留作圖痕跡．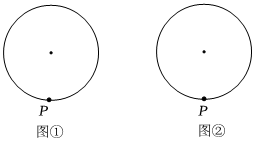
發(fā)布：2025/5/24 16:0:1組卷：115引用：1難度：0.1