十九世紀(jì)英國(guó)赫赫有名的謎題創(chuàng)作者在1903年的英國(guó)報(bào)紙上發(fā)表的“螞蟻爬行”的問(wèn)題.
問(wèn)題是:如圖1,在一個(gè)長(zhǎng)、寬、高分別為8m,8m,4m的長(zhǎng)方體房間內(nèi),一只螞蟻在右面墻的高度一半位置(即M點(diǎn)處),并且距離前面墻1m,蒼蠅正好在左面墻高度一半的位置(即N點(diǎn)處),并且距離后面墻2m,螞蟻爬到蒼蠅處應(yīng)該怎樣爬行所走路程最短,最短路程是多少m?這只螞蟻在長(zhǎng)方體表面爬行的問(wèn)題,引起了當(dāng)時(shí)很多數(shù)學(xué)愛(ài)好者的研究與討論,今天我們也一起來(lái)研究一下這個(gè)當(dāng)時(shí)非常熱門(mén)的數(shù)學(xué)問(wèn)題!
[基礎(chǔ)研究]如圖2,在長(zhǎng)、寬、高分別為a,b,c(a>b>c)的長(zhǎng)方體一個(gè)頂點(diǎn)A處有一只螞蟻,欲從長(zhǎng)方體表面爬行去另一個(gè)頂點(diǎn)C′處吃食物,探究哪種爬行路徑是最短的?
(1)觀察發(fā)現(xiàn):螞蟻從A點(diǎn)出發(fā),為了走出最短路線,根據(jù)兩點(diǎn)之間線段最短的知識(shí),并結(jié)合展開(kāi)與折疊原理,一共有3種不同的爬行路線,即圖3、圖4、圖5所示.
填空:圖5是由 左左面與 上上面展開(kāi)得到的平面圖形;
(填“前”、“后”、“左”、“右”、“上”、“下”)
(2)推理驗(yàn)證:如圖3,由勾股定理得,.AC′2=(a+b)2+c2=a2+b2+c2+2ab,
如圖4,由勾股定理得,AC′2=(b+c)2+a2=a2+b2+c2+2bc,
如圖5,AC′2=(a+c)2+b2=a2+b2+c2+2ac.
要使得AC′的值最小,
∵a>b>c
……,(請(qǐng)補(bǔ)全推理過(guò)程)
∴ab>ac>bc
∴選擇如圖 44情況,此時(shí)AC′2的值最小,則AC′的值最小,即這種爬行路徑是最短的.
[簡(jiǎn)單應(yīng)用]
如圖6,長(zhǎng)方體的長(zhǎng),寬,高分別為24cm,12cm,40cm,點(diǎn)P是FG的中點(diǎn),一只螞蟻要沿著長(zhǎng)方體的表面從點(diǎn)A爬到點(diǎn)P,則爬行的最短路程長(zhǎng)為 5050cm.
[問(wèn)題回歸]
最后讓我們?cè)倩氐侥堑朗攀兰o(jì)英國(guó)報(bào)紙上發(fā)表的“螞蟻爬行”的問(wèn)題(如圖1),那只螞蟻所走的最短路程是 1313m.

【考點(diǎn)】平面展開(kāi)-最短路徑問(wèn)題.
【答案】左;上;4;50;13
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書(shū)面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:849引用:1難度:0.3
相似題
-
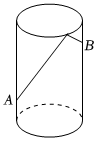
 1.如圖,圓柱的底面半徑是4,高是5,一只在A點(diǎn)的螞蟻想吃到B點(diǎn)的食物,需要爬行的最短路徑是(π取3)( )
1.如圖,圓柱的底面半徑是4,高是5,一只在A點(diǎn)的螞蟻想吃到B點(diǎn)的食物,需要爬行的最短路徑是(π取3)( )A.9 B.13 C.14 D.25 發(fā)布:2025/5/30 17:30:1組卷:1933引用:12難度:0.7 -
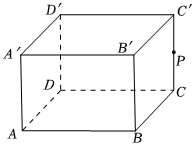 2.如圖,長(zhǎng)方體的底面是邊長(zhǎng)為6的正方形,高AA'=4,若棱CC'的中點(diǎn)P處有一只螞蟻,要沿著長(zhǎng)方體的表面爬到頂點(diǎn)A'處,則它需要爬行的最短路程是 .發(fā)布:2025/5/29 19:30:1組卷:67引用:1難度:0.5
2.如圖,長(zhǎng)方體的底面是邊長(zhǎng)為6的正方形,高AA'=4,若棱CC'的中點(diǎn)P處有一只螞蟻,要沿著長(zhǎng)方體的表面爬到頂點(diǎn)A'處,則它需要爬行的最短路程是 .發(fā)布:2025/5/29 19:30:1組卷:67引用:1難度:0.5 -
 3.如圖,圓柱形玻璃杯高為22cm,底面周長(zhǎng)為30cm,在杯內(nèi)壁離杯上沿3cm的點(diǎn)B處粘有一粒面包渣,此時(shí)一只螞蟻正好在杯外壁,離杯底5cm與面包渣相對(duì)的點(diǎn)A處,則螞蟻從外壁A處到內(nèi)壁B處的最短距離為 cm(杯壁厚度不計(jì)).發(fā)布:2025/5/30 7:30:1組卷:747引用:1難度:0.5
3.如圖,圓柱形玻璃杯高為22cm,底面周長(zhǎng)為30cm,在杯內(nèi)壁離杯上沿3cm的點(diǎn)B處粘有一粒面包渣,此時(shí)一只螞蟻正好在杯外壁,離杯底5cm與面包渣相對(duì)的點(diǎn)A處,則螞蟻從外壁A處到內(nèi)壁B處的最短距離為 cm(杯壁厚度不計(jì)).發(fā)布:2025/5/30 7:30:1組卷:747引用:1難度:0.5


