【探索發現】
（1）小明在學習等邊三角形的相關知識時，遇到這樣一個問題：如圖1，△ABC是等邊三角形，點O是△ABC的外心，D是AB邊的中點，連接OC，OD，OA，OB．猜想：①∠AOB=120120°；②OCOD的值為 22．
【猜想驗證】
（2）如圖2，若點O在等邊三角形ABC的內部運動，且∠AOB的度數和（1）中一樣，D是AB邊的中點，連接OC，OD．小明想通過三角形全等或相似來探索OCOD的值是否發生變化，下面是小明的探索過程：
OCOD的值沒有發生變化．證明如下：
以OA，OB為鄰邊構造?AEBO，在邊OC左側構造等邊三角形COF，連接AF，DE，如圖3所示．
…
請你根據以上輔助線，將后面的證明過程補充完整．
【拓展應用】
（3）在（2）的條件下，若AB=27，當OA，OB，OC三條線段組成的三角形恰好為直角三角形時，直接寫出線段OA的長．
OC
OD
OC
OD
OC
OD
AB
=
2
7
【考點】圓的綜合題．
【答案】120；2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：73引用：1難度：0.4
相似題
-
1．如圖1，在Rt△ADC中，∠ADC=90°，∠DAC=37°，AC=10，點O在邊AD上，由點D向點A運動，當點O與點A重合時，停止運動．以點O為圓心，OD為半徑在AD的下方作半圓O，半圓O與AD交于點M．（sin37°=0.6，cos37°=0.8，tan37°=0.75）
如圖1，當OD=2時，∠OCD=°，點C到半圓O的最短距離=；3
（2）半圓O與AC相切時，求OD的長？
（3）如圖2，半圓O與AC交于點E、F，當EF=6.4時，求扇形EOF的面積？
（4）以AD，DC為邊矩形ABCD，當半圓O與△ABC有兩個公共點時，則OD的取值范圍是 .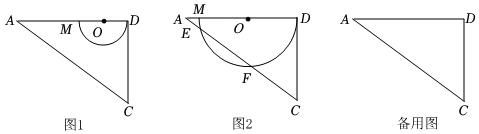
發布：2025/5/26 10:30:2組卷：830引用：2難度：0.2 -
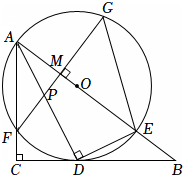2．如圖，在Rt△ABC中，∠C=90°，AD是角平分線，DE⊥AD交AB于E，△ADE的外接圓⊙O與邊AC相交于點F，過F作AB的垂線交AD于P，交AB于M，交⊙O于G，連接GE．
（1）求證：BC是⊙O的切線；
（2）若tanG=，BE=4，求⊙O的半徑；43
（3）在（2）的條件下，求AP的長．發布：2025/5/26 10:30:2組卷：240引用：1難度：0.2 -
3．如圖，在三角形中，如果一邊上存在一點將該邊分為兩條線段，且這兩條線段的積等于這個點與該邊所對頂點連線長度的平方，則稱這個點為三角形該邊的“中頂點”．
如圖1，△ABC中，點D是BC邊上一點，連接AD，若AD2=BD?CD，則稱點D是△ABC中BC邊上的“中頂點”．
（1）等腰直角三角形斜邊上的“中頂點”的個數有 個．
（2）如圖2，△ABC的頂點是4×3網格圖的格點，請僅用直尺畫出斜邊AB邊上的“中頂點”，并用字母表示．
（3）如圖3，△ABC是⊙O的內接三角形，D是BC上一點，OD⊥AD．
求證：點D是△ABC中BC邊上的“中頂點”；
證明：延長AD交⊙O于點E，連接OA、OE、CE，
在△AOE中，OA=OE，OD⊥AD
∴AD=ED，
………………（將后面證明過程補充完整）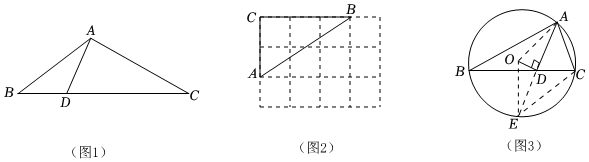
發布：2025/5/26 11:0:2組卷：97引用：1難度：0.3