通過對下面數學模型的研究學習，解決下列問題：
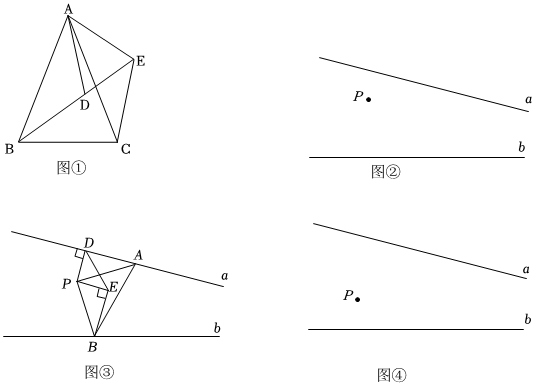
【模型理解】（1）如圖①，△ABC，△ADE共頂點A，AB=AC，AD=AE，∠BAC=∠DAE，連BD、CE．由∠BAC-∠DAC=∠DAE-∠DAC，得∠BAD=∠CAE．又AB=AC，AD=AE，可以推理得到△ABD≌△ACE，進而得到BD=CECE，∠ABD=∠ACE∠ACE；
【問題研究】（2）小明同學在思考完上述問題后，解決了下面的尺規作圖問題．如圖②，已知直線a、b及點P，a與b不平行．作等腰直角△PAB，使得點A、B分別在直線a、b上．小明同學作法簡述如下：如圖③，過點P作PD⊥a,垂足為點D，以P為直角頂點作等腰直角三角形PDE，過點E作EB⊥PE，交b于點B，在a上截取DA=BE，連接AB．△PAB即為所要求作的等腰直角三角形．請證明小明的作法是正確的；
【深入研究】小明同學經過研究發現：在上題條件下，也能作出等邊△PAB，使得點A、B分別在直線a、b上．
（3）請你簡述作法，并在圖④中畫出示意圖．（不需要尺規作圖）
【考點】三角形綜合題．
【答案】CE；∠ACE
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/16 11:0:2組卷：455引用：1難度：0.3
相似題
-
1．有公共頂點C的兩個等腰直角三角形按如圖1所示放置，點E在AB邊上．
（1）連接BD，請直接寫出值為 ；BDAE
（2）如圖2，F，G分別為AB，ED的中點，連接FG，求值；AEFG
（3）如圖3，N為BE的中點，連接CN，AD，求值．ADCN發布：2025/5/21 15:30:1組卷：280引用：1難度：0.3 -
2．如圖1，在等腰直角三角形ABC中，∠BAC=90°，點E，F分別為AB，AC的中點，H為線段EF上一動點（不與點E，F重合），將線段AH繞點A逆時針方向旋轉90°得到AG，連接GC，HB．
（1）證明：△AHB≌△AGC；
（2）如圖2，連接GF，HG，HG交AF于點Q．
①證明：在點H的運動過程中，總有∠HFG=90°；
②若AB=AC=4，當EH的長度為多少時△AQG為等腰三角形？
發布：2025/5/21 11:30:1組卷：1879引用：13難度：0.1 -
3．如圖，在△ABC中，AB=AC，∠BAC=2α（45°＜α＜90°）D是BC的中點，E是BD的中點，連接AE．將射線AE繞點A逆時針旋轉α得到射線AM，過點E作EF⊥AE交射線AM于點F．
（1）①依題意補全圖形；
②求證：∠B=∠AFE；
（2）連接CF，DF，用等式表示線段CF，DF之間的數量關系，并證明．發布：2025/5/21 13:0:1組卷：1772引用：5難度：0.3