當(dāng)前位置:
試題詳情
演繹式探究--探究點(diǎn)電荷的電場(chǎng)強(qiáng)度
如果帶電體間的距離比它們的大小大得多,這樣的帶電體可以看成是點(diǎn)電荷。
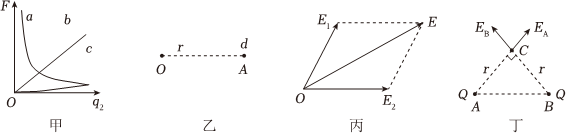
(1)實(shí)驗(yàn)發(fā)現(xiàn),帶電量分別為q1、q2的兩個(gè)點(diǎn)電荷距離為r時(shí),它們之間的作用力F=kq1q2r2,其中k為常量。當(dāng)q1和r一定時(shí),F(xiàn)與q2之間的關(guān)系圖象可以用圖甲中的圖線cc來(lái)表示。
(2)磁體周?chē)嬖诖艌?chǎng),同樣,電荷周?chē)泊嬖陔妶?chǎng)。電場(chǎng)對(duì)放入其中的電荷產(chǎn)生電場(chǎng)力的作用。點(diǎn)電荷q1與q2之間的作用力實(shí)際是q1(或q2)的電場(chǎng)對(duì)q2(或q1)的電場(chǎng)力。物理學(xué)中規(guī)定:放入電場(chǎng)中某一點(diǎn)的電荷受到的電場(chǎng)力F跟它的電量q的比值,叫做該點(diǎn)的電場(chǎng)強(qiáng)度,用E表示,則E=FqFq。
如圖乙所示,在距離點(diǎn)電荷Q為r的A點(diǎn)放一個(gè)點(diǎn)電荷q,則點(diǎn)電荷q受到的電場(chǎng)力F=kQqr2kQqr2,點(diǎn)電荷Q在A點(diǎn)產(chǎn)生的電場(chǎng)強(qiáng)度EA=kQr2kQr2。
(3)如果兩個(gè)點(diǎn)電荷同時(shí)存在,它們的電場(chǎng)會(huì)互相疊加,形成合電場(chǎng)。如圖丙所示,兩個(gè)互成角度的電場(chǎng)強(qiáng)度E1和E2,它們合成后的電場(chǎng)強(qiáng)度E用平行四邊形的對(duì)角線表示。如圖丁所示,兩個(gè)點(diǎn)電荷Q分別放在A、B兩點(diǎn),AC=BC=r,AB=2r它們?cè)贑點(diǎn)產(chǎn)生的合電場(chǎng)強(qiáng)度為E合大小為2kQr22kQr2
q
1
q
2
r
2
F
q
F
q
Q
q
r
2
Q
q
r
2
k
Q
r
2
k
Q
r
2
2
2
k
Q
r
2
2
k
Q
r
2
【答案】c;;k;;
F
q
Q
q
r
2
k
Q
r
2
2
k
Q
r
2
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書(shū)面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/4/20 14:35:0組卷:139引用:3難度:0.3
相似題
-
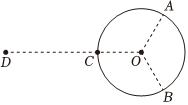 1.半徑為R的絕緣細(xì)圓環(huán)固定在圖示位置,圓心位于O點(diǎn),環(huán)上均勻分布著電量為Q的正電荷。點(diǎn)A、B、C將圓環(huán)三等分,取走A、B處兩段弧長(zhǎng)均為ΔL的小圓弧上的電荷。將一點(diǎn)電荷q置于OC延長(zhǎng)線上距C點(diǎn)為2R的D點(diǎn),O點(diǎn)的電場(chǎng)強(qiáng)度剛好為零。圓環(huán)上剩余電荷分布不變,則q為( )
1.半徑為R的絕緣細(xì)圓環(huán)固定在圖示位置,圓心位于O點(diǎn),環(huán)上均勻分布著電量為Q的正電荷。點(diǎn)A、B、C將圓環(huán)三等分,取走A、B處兩段弧長(zhǎng)均為ΔL的小圓弧上的電荷。將一點(diǎn)電荷q置于OC延長(zhǎng)線上距C點(diǎn)為2R的D點(diǎn),O點(diǎn)的電場(chǎng)強(qiáng)度剛好為零。圓環(huán)上剩余電荷分布不變,則q為( )A.正電荷, q=2QΔLπRB.正電荷, q=9QΔL2πRC.負(fù)電荷, q=2QΔLπRD.負(fù)電荷, q=9QΔL2πR發(fā)布:2024/12/18 15:0:1組卷:315引用:3難度:0.7 -
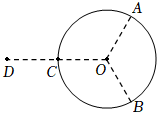 2.半徑為R的絕緣細(xì)圓環(huán)固定在圖示位置,圓心位于O點(diǎn),環(huán)上均勻分布著電量為Q的正電荷。點(diǎn)A、B、C將圓環(huán)三等分,取走A、B處兩段弧長(zhǎng)均為ΔL的小圓弧上的電荷。將一點(diǎn)電荷q置于OC延長(zhǎng)線上距O點(diǎn)為2R的D點(diǎn),O點(diǎn)的電場(chǎng)強(qiáng)度剛好為零。圓環(huán)上剩余電荷分布不變,q為( )
2.半徑為R的絕緣細(xì)圓環(huán)固定在圖示位置,圓心位于O點(diǎn),環(huán)上均勻分布著電量為Q的正電荷。點(diǎn)A、B、C將圓環(huán)三等分,取走A、B處兩段弧長(zhǎng)均為ΔL的小圓弧上的電荷。將一點(diǎn)電荷q置于OC延長(zhǎng)線上距O點(diǎn)為2R的D點(diǎn),O點(diǎn)的電場(chǎng)強(qiáng)度剛好為零。圓環(huán)上剩余電荷分布不變,q為( )A.正電荷, q=QΔLπRB.正電荷, q=3QΔLπRC.負(fù)電荷, q=2QΔLπRD.負(fù)電荷, q=23QΔLπR發(fā)布:2024/12/29 16:30:1組卷:2306引用:10難度:0.5 -
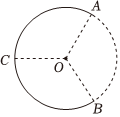 3.如圖所示,半徑為R的絕緣細(xì)圓環(huán)上均勻分布著電荷量為Q的正電荷,A、B、C三點(diǎn)將圓周三等分。取走A、B處弧長(zhǎng)均為ΔL的圓弧上的電荷(ΔL?R),靜電力常量為k,此時(shí)圓心O處電場(chǎng)強(qiáng)度( )
3.如圖所示,半徑為R的絕緣細(xì)圓環(huán)上均勻分布著電荷量為Q的正電荷,A、B、C三點(diǎn)將圓周三等分。取走A、B處弧長(zhǎng)均為ΔL的圓弧上的電荷(ΔL?R),靜電力常量為k,此時(shí)圓心O處電場(chǎng)強(qiáng)度( )A.方向沿CO,大小為 kQΔL2πR3B.方向沿OC,大小為 kQΔL2πR3C.方向沿CO,大小為 kQΔLπR3D.方向沿OC,大小為 kQΔLπR3發(fā)布:2024/12/15 20:0:1組卷:285引用:3難度:0.6


