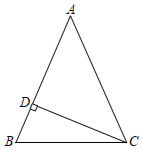
求證：頂角是銳角的等腰三角形腰上的高與底邊夾角等于其頂角的一半．根據條件和結論，結合圖形，用符號語言補充寫出“已知”和“求證”．
已知：在△ABC中，∠A為銳角，AB=AC，CD⊥AB于DCD⊥AB于D．
求證：∠BCD=12∠A∠BCD=12∠A．
證明：過點A作AE⊥BC于E，
∵AB=AC，
∴∠BAE=∠CE=12∠BAC，
∵AE⊥BC，
∴∠BAE+∠B=90°，
∵CD⊥AB，
∴∠BCD+∠B=90°，
∴∠BCD=∠BAE=12∠BAC過點A作AE⊥BC于E，
∵AB=AC，
∴∠BAE=∠CE=12∠BAC，
∵AE⊥BC，
∴∠BAE+∠B=90°，
∵CD⊥AB，
∴∠BCD+∠B=90°，
∴∠BCD=∠BAE=12∠BAC．
1
2
1
2
∵AB=AC，
∴∠BAE=∠CE=
1
2
∵AE⊥BC，
∴∠BAE+∠B=90°，
∵CD⊥AB，
∴∠BCD+∠B=90°，
∴∠BCD=∠BAE=
1
2
∵AB=AC，
∴∠BAE=∠CE=
1
2
∵AE⊥BC，
∴∠BAE+∠B=90°，
∵CD⊥AB，
∴∠BCD+∠B=90°，
∴∠BCD=∠BAE=
1
2
【考點】等腰三角形的性質．
【答案】CD⊥AB于D；∠BCD=∠A；過點A作AE⊥BC于E，
∵AB=AC，
∴∠BAE=∠CE=∠BAC，
∵AE⊥BC，
∴∠BAE+∠B=90°，
∵CD⊥AB，
∴∠BCD+∠B=90°，
∴∠BCD=∠BAE=∠BAC
1
2
∵AB=AC，
∴∠BAE=∠CE=
1
2
∵AE⊥BC，
∴∠BAE+∠B=90°，
∵CD⊥AB，
∴∠BCD+∠B=90°，
∴∠BCD=∠BAE=
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/5 6:30:2組卷：446引用：5難度：0.6
