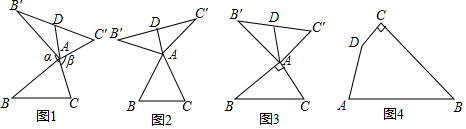
我們定義：如圖1，在△ABC中，把AB繞點(diǎn)A順時(shí)針旋轉(zhuǎn)α（0°＜α＜180°）得到AB'，把AC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)β得到AC'，連接B'C'．當(dāng)α+β=180°時(shí)，我們稱△A'B'C'是△ABC的“旋補(bǔ)三角形”，△AB'C'邊B'C'上的中線AD叫做△ABC的“旋補(bǔ)中線”，點(diǎn)A叫做“旋補(bǔ)中心”．
特例感知：
（1）在圖2，圖3中，△AB'C'是△ABC的“旋補(bǔ)三角形”，AD是△ABC的“旋補(bǔ)中線”．
①如圖2，當(dāng)△ABC為等邊三角形時(shí)，AD與BC的數(shù)量關(guān)系為AD=1212BC；
②如圖3，當(dāng)∠BAC=90°，BC=8時(shí)，則AD長為 44．
猜想論證：
（2）在圖1中，當(dāng)△ABC為任意三角形時(shí)，猜想AD與BC的數(shù)量關(guān)系，并給予證明．
拓展應(yīng)用
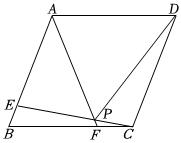
（3）如圖4，在四邊形ABCD，∠C=90°，∠D=150°，BC=12，CD=23，DA=6．在四邊形內(nèi)部是否存在點(diǎn)P，使△PDC是△PAB的“旋補(bǔ)三角形”？若存在，給予證明，并求△PAB的“旋補(bǔ)中線”長；若不存在，說明理由．
1
2
1
2
3
【考點(diǎn)】四邊形綜合題．
【答案】；4
1
2
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2025/5/22 18:30:2組卷：3824引用：11難度：0.1
相似題
-
1．如圖，在平面直角坐標(biāo)系xOy中，正方形ABCD中心在原點(diǎn)，且頂點(diǎn)A的坐標(biāo)為（1，1）．動(dòng)點(diǎn)P、Q分別從點(diǎn)A、B同時(shí)出發(fā)，繞著正方形的邊按順時(shí)針方向運(yùn)動(dòng)，當(dāng)P點(diǎn)回到A點(diǎn)時(shí)兩點(diǎn)同時(shí)停止運(yùn)動(dòng)，運(yùn)動(dòng)時(shí)間為t秒．連接OP、OQ，線段OP、OQ與正方形的邊圍成的面積較小部分的圖形記為M．
（1）請寫出B、C、D點(diǎn)的坐標(biāo)；
（2）若P、Q的速度均為1個(gè)單位長度/秒，試判斷在運(yùn)動(dòng)過程中，M的面積是否發(fā)生變化，如果不變求出該值，如果變化說明理由；
（3）若P點(diǎn)速度為2個(gè)單位長度/秒，Q點(diǎn)為1個(gè)單位長度/秒，當(dāng)M的面積為時(shí)，求t的23
值．發(fā)布：2025/5/23 9:0:2組卷：270引用：2難度：0.1 -
2．已知菱形ABCD中，∠BAD=120°，點(diǎn)E、F分別在AB、BC上，BE=CF，AF與CE交于點(diǎn)P．
（1）求證：∠APE=60°；
（2）當(dāng)PC=1，PA=5時(shí)，求PD的長；
（3）當(dāng)AB=2時(shí)，求PD的最大值．3發(fā)布：2025/5/23 9:30:1組卷：176引用：3難度：0.5 -
3．某數(shù)學(xué)興趣小組在數(shù)學(xué)課外活動(dòng)中，對多邊形內(nèi)兩條互相垂直的線段做了如下探究：
（1）如圖1，在正方形ABCD中，E，F(xiàn)分別是AB，AD上的兩點(diǎn)，連接DE，CF，若DE⊥CF，求證：CF=DE．
（2）如圖2，在矩形ABCD中，過點(diǎn)C作CE⊥BD交AD于點(diǎn)E，若tan∠DCE=，求23的值．CEBD
（3）如圖3，在四邊形ABCD中，∠A=∠B=90°，E為AB上一點(diǎn)，連接DE，過點(diǎn)C作DE的垂線交ED的延長線于點(diǎn)G，交AD的延長線于點(diǎn)F，且AB=5，AD=3，CF=7．求DE的長．發(fā)布：2025/5/23 9:30:1組卷：331引用：3難度：0.4
相關(guān)試卷