黔東南州某超市購進一批商品,該商品的進價為每件30元,如果售價按每件40元出售,每個月可賣出300件.市場調查發現:這種商品的售價每上漲2元,每月少賣10件,如果超市決定該商品每件的售價高于40元但不超過60元,設每件商品的售價為x元,每月的銷售量為y件.
(1)寫出y與x的函數關系式;
(2)設每月的銷售利潤為w元,請寫出w與x的函數關系式;
(3)該商品的銷售單價定為多少時,每月的銷售利潤最大?最大利潤是多少?
【考點】二次函數的應用.
【答案】(1)y與x的函數關系式為y=-5x+500(40<x≤60);
(2)w與x的函數關系式為w=-5x2+650x-15000;
(3)該商品的售價定為60元時,每月的銷售利潤最大,最大利潤是6000元.
(2)w與x的函數關系式為w=-5x2+650x-15000;
(3)該商品的售價定為60元時,每月的銷售利潤最大,最大利潤是6000元.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/5/30 22:30:1組卷:264引用:1難度:0.6
相似題
-
1.為滿足市場需求,某超市在五月初五“端午節”來臨前夕,購進一種品牌粽子,每盒進價是40元.超市規定每盒售價不得少于45元.根據以往銷售經驗發現;當售價定為每盒45元時,每天可以賣出700盒,每盒售價每提高1元,每天要少賣出20盒.
(1)試求出每天的銷售量y(盒)與每盒售價x(元)之間的函數關系式;
(2)當每盒售價定為多少元時,每天銷售的利潤P(元)最大?最大利潤是多少?
(3)為穩定物價,有關管理部門限定:這種粽子的每盒售價不得高于58元.如果超市想要每天獲得不低于6000元的利潤,那么超市每天至少銷售粽子多少盒?發布:2025/6/1 5:0:1組卷:17967引用:103難度:0.5 -
2.大學生小張利用暑假50天在一超市勤工儉學,被安排銷售一款成本為40元/件的新型商品,此類新型商品在第x天的銷售量p件與銷售的天數x的關系如下表:
銷售單價q(元/件)與x滿足:當1≤x<25時q=x+60;當25≤x≤50時q=40+x(天) 1 2 3 … 50 p(件) 118 116 114 … 20 .1125x
(1)請分析表格中銷售量p與x的關系,求出銷售量p與x的函數關系.
(2)求該超市銷售該新商品第x天獲得的利潤y元關于x的函數關系式.
(3)這50天中,該超市第幾天獲得利潤最大?最大利潤為多少?發布:2025/6/1 5:0:1組卷:1359引用:63難度:0.5 -
3.如圖,有長為30m的籬笆,一面利用墻(墻的最大可用長度為10m),圍成中間隔有一道籬笆(平行于AB)的長方形花圃.
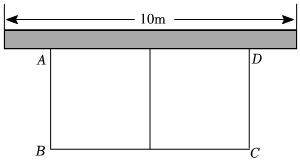
(1)設花圃的一邊AB為x m,花圃的面積為S m2,請寫出S與x的函數關系式,以及自變量x的取值范圍;
(2)當AB的長是多少米時,圍成的花圃面積為63平方米?
(3)能圍成比63平方米更大的花圃嗎?如果能,請求出最大的面積.如果不能,請說明理由.發布:2025/6/1 6:0:1組卷:370引用:1難度:0.6


