用各種盛水容器可以制作精致的家用流水景觀（如圖1）．
科學原理：如圖2，始終盛滿水的圓柱體水桶水面離地面的高度為H（單位：cm），如果在離水面豎直距離為h（單位：cm）的地方開大小合適的小孔，那么從小孔射出水的射程（水流落地點離小孔的水平距離）s（單位：cm）與h的關系式為s2=4h（H-h）．
應用思考：現用高度為20cm的圓柱體塑料水瓶做相關研究，水瓶直立地面，通過連續注水保證它始終盛滿水，在離水面豎直距離hcm處開一個小孔．
（1）寫出s2與h的關系式；并求出當h為何值時，射程s有最大值，最大射程是多少？
（2）在側面開兩個小孔，這兩個小孔離水面的豎直距離分別為a,b,要使兩孔射出水的射程相同，求a,b之間的關系式；
（3）如果想通過墊高塑料水瓶，使射出水的最大射程增加16cm,求墊高的高度及小孔離水面的豎直距離．
【考點】二次函數的應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/10 8:0:8組卷：3404引用：16難度：0.4
相似題
-
1．如圖1，是拋物線形的拱橋，當拱頂高離水面2米時，水面寬4米．如圖建立平面直角坐標系，解答下列問題：
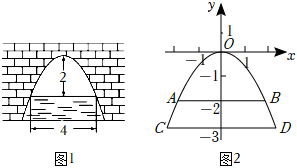
（1）如圖2，求該拋物線的函數解析式．
（2）當水面AB下降1米，到CD處時，水面寬度增加多少米？（保留根號）
（3）當水面AB上升1米時，水面寬度減少多少米？（保留根號）發布：2025/5/24 11:0:1組卷：944引用：7難度：0.5 -
2．同學們在操場上玩跳大繩的游戲，跳大繩時，繩甩到最高處的形狀是拋物線，正在甩繩的甲、乙兩名同學拿繩的手間距AB為6米，到地面的距離AO與BD均為0.9米，繩子甩到最高點C處時，最高點距地面的垂直距離為1.8m,距甲同學拿繩的手的水平距離為3m.以點O為原點建立如圖所示的平面直角坐標系．
（1）求此拋物線的解析式；
（2）如果身高為1.7m的嘉嘉站在OD之間，當繩子甩到最高處，求嘉嘉站在距點O的水平距離為多少時，繩子剛好通過他的頭頂上方．發布：2025/5/24 9:30:2組卷：179引用：1難度：0.6 -
3．某廠家生產一批遮陽傘，每個遮陽傘的成本價是20元，試銷售時發現：遮陽傘每天的銷售量y（個）與銷售單價x（元）之間是一次函數關系，當銷售單價為28元時，每天的銷售量為260個；當銷售單價為30元時，每天的銷售量為240個．
（1）求遮陽傘每天的銷出量y（個）與銷售單價x（元）之間的函數關系式；
（2）設遮陽傘每天的銷售利潤為w（元），當銷售單價定為多少元時，才能使每天的銷售利潤最大？最大利潤是多少元？發布：2025/5/24 10:0:2組卷：2127引用：13難度：0.6