2022年12月6日全國各地放開對新冠疫情的管控，在強大的祖國庇護下平穩抗疫三年的中國人民迎來了與新冠變異毒株奧密克戎的首次正面交鋒．某市為了更好的了解全體中小學生感染新冠感冒后的情況，以便及時補充醫療資源．從全市中小學生中隨機抽取了100名抗原檢測為陽性的中小學生監測其健康狀況，100名中小學生感染奧密克戎后的疼痛指數為X，并以此為樣本得到了如下圖所示的表格：
| 疼痛指數X | X≤10 | 10＜X＜90 | X≥90 |
| 人數（人） | 10 | 81 | 9 |
| 名稱 | 無癥狀感染者 | 輕癥感染者 | 重癥感染者 |
（1）統計學中常用L=
P
（
B
|
A
）
P
（
B
|
A
）
（2）若該市所有抗原檢測為陽性的中小學生的疼痛指數X近似的服從正態分布N（50，σ2），且
P
（
X
≥
90
）
=
1
10
【考點】離散型隨機變量的均值（數學期望）．
【答案】（1）；
（2）分布列見解析，數學期望E（Y）=2.4．
1
9
（2）分布列見解析，數學期望E（Y）=2.4．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/8 8:0:10組卷：422引用：12難度：0.5
相似題
-
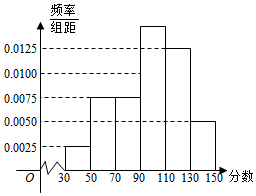1．某市舉行“中學生詩詞大賽”，分初賽和復賽兩個階段進行，規定：初賽成績大于90分的具有復賽資格，某校有800名學生參加了初賽，所有學生的成績均在區間（30，150]內，其頻率分布直方圖如圖．
（Ⅰ）求獲得復賽資格的人數；
（Ⅱ）從初賽得分在區間（110，150]的參賽者中，利用分層抽樣的方法隨機抽取7人參加學校座談交流，那么從得分在區間（110，130]與（130，150]各抽取多少人？
（Ⅲ）從（Ⅱ）抽取的7人中，選出3人參加全市座談交流，設X表示得分在區間（130，150]中參加全市座談交流的人數，求X的分布列及數學期望E（X）．發布：2024/12/29 13:30:1組卷：133引用：7難度：0.5 -
2．設離散型隨機變量X的分布列如表：
若離散型隨機變量Y=-3X+1，且E（X）=3，則（ ）X 1 2 3 4 5 P m 0.1 0.2 n 0.3 發布：2024/12/29 13:0:1組卷：198引用：6難度：0.5 -
3．從4名男生和2名女生中任選3人參加演講比賽，用X表示所選3人中女生的人數，則E（X）為（ ）
發布：2024/12/29 13:30:1組卷：138引用：6難度：0.7