問題提出:
如圖,圖①是一張由三個(gè)邊長(zhǎng)為1的小正方形組成的“L”形紙片,圖②是一張a×b的方格紙(a×b的方格紙指邊長(zhǎng)分別為a,b的矩形,被分成a×b個(gè)邊長(zhǎng)為1的小正方形,其中a≥2,b≥2,且a,b為正整數(shù)).把圖①放置在圖②中,使它恰好蓋住圖②中的三個(gè)小正方形,共有多少種不同的放置方法?
問題探究:
為探究規(guī)律,我們采用一般問題特殊化的策略,先從最簡(jiǎn)單的情形入手,再逐次遞進(jìn),最后得出一般性的結(jié)論.
探究一:
把圖①放置在2×2的方格紙中,使它恰好蓋住其中的三個(gè)小正方形,共有多少種不同的放置方法?
如圖③,對(duì)于2×2的方格紙,要用圖①蓋住其中的三個(gè)小正方形,顯然有4種不同的放置方法.
探究二:
把圖①放置在3×2的方格紙中,使它恰好蓋住其中的三個(gè)小正方形,共有多少種不同的放置方法?
如圖④,在3×2的方格紙中,共可以找到2個(gè)位置不同的2×2方格,依據(jù)探究一的結(jié)論可知,把圖①放置在3×2的方格紙中,使它恰好蓋住其中的三個(gè)小正方形,共有2×4=8種不同的放置方法.

(1)探究三:
把圖①放置在a×2的方格紙中,使它恰好蓋住其中的三個(gè)小正方形,共有多少種不同的放置方法?
如圖⑤,在a×2的方格紙中,共可以找到個(gè)位置不同的2×2方格,依據(jù)探究一的結(jié)論可知,把圖①放置在a×2的方格紙中,使它恰好蓋住其中的三個(gè)小正方形,共有 (a-1)(a-1)種不同的放置方法.
(2)探究四:
把圖①放置在a×3的方格紙中,使它恰好蓋住其中的三個(gè)小正方形,共有多少種不同的放置方法?
如圖⑥,在a×3的方格紙中,共可以找到個(gè)位置不同的2×2方格,依據(jù)探究一的結(jié)論可知,把圖①放置在a×3的方格紙中,使它恰好蓋住其中的三個(gè)小正方形,共有 (4a-4)(4a-4)種不同的放置方法.
(3)問題解決:
把圖①放置在a×b的方格紙中,使它恰好蓋住其中的三個(gè)小正方形,共有多少種不同的放置方法?(仿照前面的探究方法,寫出解答過程,不需畫圖)
(4)問題拓展:
如圖,圖⑦是一個(gè)由4個(gè)棱長(zhǎng)為1的小立方體構(gòu)成的幾何體,圖⑧是一個(gè)長(zhǎng)、寬、高分別為a,b,c(a≥2,b≥2,c≥2,且a,b,c是正整數(shù))的長(zhǎng)方體,被分成了a×b×c個(gè)棱長(zhǎng)為1的小立方體.在圖⑧的不同位置共可以找到個(gè)圖⑦這樣的幾何體.
【答案】(a-1);(4a-4)
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/8/24 6:0:10組卷:33引用:1難度:0.5
相似題
-
1.下面是按照一定規(guī)律畫出的一系列“樹枝”經(jīng)觀察,圖(2)比圖(1)多出2個(gè)“樹枝”,圖(3)比圖(2)多出4個(gè)“樹枝”,圖(4)比圖(3)多出8個(gè)“樹枝”,按此規(guī)律,圖(7)比圖(6)多出個(gè)樹枝.
 發(fā)布:2025/5/28 1:0:2組卷:65引用:2難度:0.3
發(fā)布:2025/5/28 1:0:2組卷:65引用:2難度:0.3 -
2.把一張紙剪成5塊,從所得紙片中取出若干塊各剪成5塊,再從以上所得紙片中取出若干塊,每塊又剪成5塊,…,如此進(jìn)行下去,到剪完某一次后停止時(shí),所得紙片總數(shù)可能是( )
A.2002 B.2003 C.2004 D.2005 發(fā)布:2025/5/28 1:30:2組卷:26引用:2難度:0.9 -
3.(1)圖(1)是正方體木塊,把它切去一塊,可能得到形如圖(2),(3),(4)(5)的木塊.
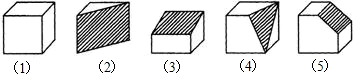
我們知道,圖(1)的正方體木塊有8個(gè)頂點(diǎn),12條棱,6個(gè)面,請(qǐng)你將圖(2),(3),(4),(5)中木塊的頂點(diǎn)數(shù),棱數(shù),面數(shù)填入下表:
(2)觀察上表,請(qǐng)你歸納上述各種木塊的頂點(diǎn)數(shù),棱數(shù),面數(shù)之間的數(shù)量關(guān)系,這種數(shù)量關(guān)系是:.圖 頂點(diǎn)數(shù) 棱數(shù) 面數(shù) (1) 8 12 6 (2) (3) (4) (5)
(3)如圖,是用虛線畫出的正方體木塊,請(qǐng)你想象一種與圖(2)~(5)不同的切法,把切去一塊后得到的那一塊的每條棱都改畫成實(shí)線,則該木塊的頂點(diǎn)數(shù)為 ,棱數(shù)為 ,面數(shù)為 .這與你(2)題中所歸納的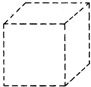 關(guān)系是否相符?發(fā)布:2025/5/28 1:30:2組卷:194引用:4難度:0.3
關(guān)系是否相符?發(fā)布:2025/5/28 1:30:2組卷:194引用:4難度:0.3


