綜合與實踐
問題情境：
數(shù)學課上，同學們以“長方形紙帶的折疊”為主題開展數(shù)學活動，已知長方形紙帶的邊AD∥BC，將紙片沿折痕EF折疊，點A，B分別為點A'，B'，線段B′F與DE交于點G．（說明：折疊后紙帶的邊A′E∥B′F始終成立）
操作探究：
（1）如圖1，若B′F⊥AD，則∠EFG的度數(shù)為 4545°．
（2）如圖2，改變折痕EF的位置，其余條件不變，小彬發(fā)現(xiàn)圖中∠1=∠2始終成立，請說明理由；
（3）改變折痕EF的位置，使點B'恰好落在線段AD上，然后繼續(xù)沿折痕MN折疊紙帶，點M，N分別在線段FC和B′D上．
A．如圖3，點C的對應點與點B'重合，點D的對應點為點D′．若∠BFE=70°，∠CMN=80°，直接寫出∠FB′M的度數(shù)．
B．如圖4，點C，D的對應點分別為點C′，D′，點C′，D′均在AD上方，若∠BFE=α，∠CMN=β，當FB′∥MC′時，直接寫出α與β之間的數(shù)量關系．
【考點】四邊形綜合題．
【答案】45
【解答】
【點評】
聲明：本試題解析著作權屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：311引用：6難度：0.2
相似題
-
1．在四邊形ABCD中，AB=BC，∠B=90°；
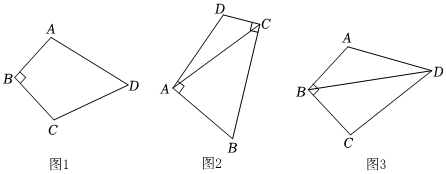
（1）如圖1，已知∠D=60°，則∠A+∠C的度數(shù)等于 °；
（2）如圖2，在四邊形ABCD中，AB=AD，∠BAD=∠BCD=90°，連接AC．若AC=6，求四邊形ABCD的面積；
（3）如圖3，已知AB=BC，∠ADC=60°，∠B=90°，AD=4，CD=4，求線段BD的長度．3發(fā)布：2025/5/24 3:30:1組卷：199引用：1難度：0.5 -
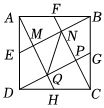2．如圖，點E，F(xiàn)，G，H分別是正方形ABCD的邊DA，AB，BC，CD的中點，連接AH，BE，CF，DG，它們分別相交于點M，N，P，Q，連接NQ．若AB=4，則下列結(jié)論錯誤的是（ ）發(fā)布：2025/5/24 4:0:7組卷：148引用：1難度：0.2 -
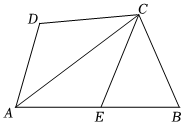3．如圖，在四邊形ABCD中，AD=11，BC=CD=13，對角線AC=20，點E是AB邊上一點，連接CE．
（1）若AB＞AD且AC平分∠DAB，
①當AE=AD時，求證：CE=BC；
②求線段CE的最小值；
（2）當點E是AB邊的中點，且CE=BC時，直接寫出△ABC的面積．12發(fā)布：2025/5/24 3:0:1組卷：152引用：1難度：0.4