定義：如果一個(gè)四邊形的一組對(duì)角互余，那么我們稱這個(gè)四邊形為“對(duì)角互余四邊形”．
（1）如圖1，在對(duì)角互余四邊形ABCD中，∠D=30°，且AC⊥BC，AC⊥AD．若BC=1，求四邊形ABCD的面積和周長(zhǎng)．
（2）如圖2，在四邊形ABCD中，連接AC，∠BAC=90°，點(diǎn)O是△ACD外接圓的圓心，連接OA，∠OAC=∠ABC，求證：四邊形ABCD是“對(duì)角互余四邊形”；
（3）在（2）的條件下，如圖3，已知AD=4，DC=10，AB=3AC，連接BD，求線段BD的長(zhǎng)．
DC
=
10
【考點(diǎn)】圓的綜合題．
【答案】（1）四邊形ABCD的面積為2，周長(zhǎng)為6+2；
（2）證明見(jiàn)解答；
（3）線段BD的長(zhǎng)是5．
3
3
（2）證明見(jiàn)解答；
（3）線段BD的長(zhǎng)是5
10
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/4/20 14:35:0組卷：405引用：2難度：0.3
相似題
-
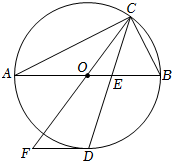1．如圖，點(diǎn)C在以AB為直徑的⊙O上，CD平分∠ACB交⊙O于點(diǎn)D，交AB于點(diǎn)E，過(guò)點(diǎn)D作⊙O的切線交CO的延長(zhǎng)線于點(diǎn)F．
（1）求證：FD∥AB；
（2）若AC=2，BC=5，求FD的長(zhǎng)．5發(fā)布：2025/5/23 0:30:1組卷：2147引用：13難度：0.2 -
2．已知：四邊形ABCD內(nèi)接于⊙O，AC、BD即相交于點(diǎn)F，連接OC，∠BCO=∠ABD．
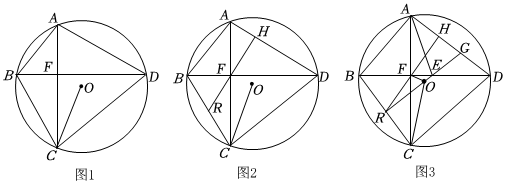
（1）如圖1，求證：AC⊥BD；
（2）如圖2，過(guò)點(diǎn)F作FH⊥AD于點(diǎn)H，延長(zhǎng)HF交BC于點(diǎn)R．求證：BR=CR；
（3）如圖3，在（2）的條件下，點(diǎn)E、點(diǎn)G分別是FD，AD上的點(diǎn)，連接AE、EG、OR，∠ADB=2∠CAE，，EF=2，EG=DG=154，求⊙O的半徑．tan∠FOR=76發(fā)布：2025/5/22 23:30:1組卷：131引用：1難度：0.3 -
3．在平面直角坐標(biāo)系xOy中，已知點(diǎn)M（a,b），N．
對(duì)于點(diǎn)P給出如下定義：將點(diǎn)P向右（a≥0）或向左（a＜0）平移|a|個(gè)單位長(zhǎng)度，再向上（b≥0）或向下（b＜0）平移|b|個(gè)單位長(zhǎng)度，得到點(diǎn)P'，點(diǎn)P'關(guān)于點(diǎn)N的對(duì)稱點(diǎn)為P″，NP″中點(diǎn)記為Q，稱點(diǎn)Q為點(diǎn)P的“對(duì)應(yīng)點(diǎn)”．
（1）如圖，點(diǎn)M（1，1），點(diǎn)N在線段OM的延長(zhǎng)線上，若點(diǎn)P（-3，0），點(diǎn)Q為點(diǎn)P的“對(duì)應(yīng)點(diǎn)”．
①在圖1中畫(huà)出點(diǎn)Q；
②連接PQ，交線段ON于點(diǎn)T．求證：；NT=13OM
（2）⊙O的半徑為2，M是⊙O上一點(diǎn)，點(diǎn)N在線段OM上，且ON=t（1＜t＜2），若P為⊙O外一點(diǎn)，點(diǎn)Q為點(diǎn)P的“對(duì)應(yīng)點(diǎn)”，連接PQ．當(dāng)點(diǎn)M在⊙O上運(yùn)動(dòng)時(shí)，直接寫(xiě)出PQ長(zhǎng)的最大值與最小值的差（用含t的式子表示）．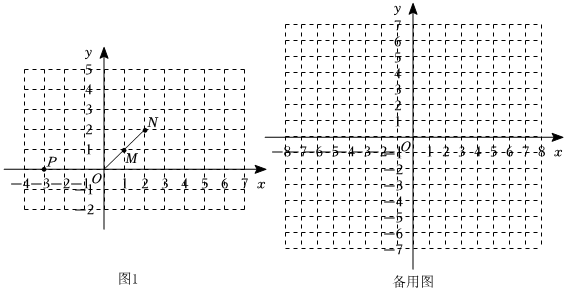
發(fā)布：2025/5/23 0:0:1組卷：176引用：1難度：0.3