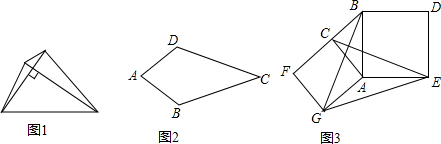
如圖1，我們把對角線互相垂直的四邊形叫做垂美四邊形．
（1）概念理解：如圖2，在四邊形ABCD中，AB=AD，CB=CD，問四邊形ABCD是垂美四邊形嗎？請說明理由．
（2）性質(zhì)探究：試探索垂美四邊形ABCD兩組對邊AB，CD與BC，AD之間的數(shù)量關(guān)系．
猜想結(jié)論：（要求用文字語言敘述） 垂美四邊形兩組對邊的平方和相等垂美四邊形兩組對邊的平方和相等
寫出證明過程（先畫出圖形，寫出已知、求證）．
（3）問題解決：如圖3，分別以Rt△ACB的直角邊AC和斜邊AB為邊向外作正方形ACFG和正方形ABDE，連接CE，BG，GE，已知AC=4，AB=5，求GE長．
【考點(diǎn)】四邊形綜合題．
【答案】垂美四邊形兩組對邊的平方和相等
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：2670引用：21難度：0.1
相似題
-
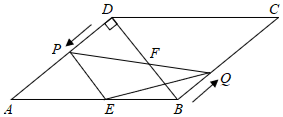1．如圖，在?ABCD中，∠ADB=90°，AB=10cm,AD=8cm,點(diǎn)P從點(diǎn)D出發(fā)，沿DA方向勻速運(yùn)動，速度為2cm/s；同時，點(diǎn)Q從點(diǎn)B出發(fā)，沿BC方向勻速運(yùn)動，速度為1cm/s.當(dāng)一個點(diǎn)停止運(yùn)動，另一個點(diǎn)也停止運(yùn)動．過點(diǎn)P作PE∥BD交AB于點(diǎn)E，連接PQ，交BD于點(diǎn)F．設(shè)運(yùn)動時間為t（s）（0＜t＜4）．解答下列問題：
（1）當(dāng)t為何值時，PQ∥AB？
（2）連接EQ，設(shè)四邊形APQE的面積為y（cm2），求y與t的函數(shù)關(guān)系式．
（3）當(dāng)t為何值時，點(diǎn)E在線段PQ的垂直平分線上？
（4）若點(diǎn)F關(guān)于AB的對稱點(diǎn)為F′，是否存在某一時刻t,使得點(diǎn)P，E，F(xiàn)′三點(diǎn)共線？若存在，求出t的值；若不存在，請說明理由．發(fā)布：2025/5/23 2:30:1組卷：955引用：5難度：0.3 -
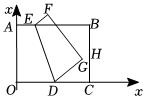2．如圖，在平面直角坐標(biāo)系中，矩形ABCO的頂點(diǎn)B的坐標(biāo)為（4，3），D為OC的中點(diǎn)，E是AB上一動點(diǎn)，將四邊形OAED沿ED折疊，使點(diǎn)A落在F處，點(diǎn)O落在G處，當(dāng)線段DG的延長線恰好經(jīng)過BC的中點(diǎn)H時，點(diǎn)F的坐標(biāo)為（ ）發(fā)布：2025/5/23 3:0:1組卷：232引用：1難度：0.3 -
3．【問題提出】
（1）如圖①，在平行四邊形ABCD中，對角線AC、BD相交于點(diǎn)O，若S△ABC=3，則△ABD的面積為 ；
【問題探究】
（2）如圖②，已知BC=6，點(diǎn)A為BC上方的一個動點(diǎn)，且∠BAC=120°，點(diǎn)D為BA延長線上一點(diǎn)，且AD=AC，連接CD，求△BCD面積的最大值；
【問題解決】
（3）如圖③，四邊形ABCD是規(guī)劃中的休閑廣場示意圖，AC、BD為兩條人行通道，根據(jù)規(guī)劃要求，人行通道AC的長為500米，∠DBC=30°，AD∥BC，為了容納更多的人，要求該休閑廣場的面積盡可能大，請問休閑廣場ABCD的面積是否存在最大值，如果存在，求出四邊形ABCD的最大面積，如果不存在，請說明理由．（結(jié)果保留根號）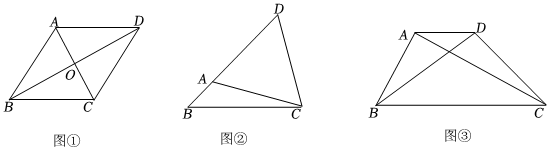
發(fā)布：2025/5/23 3:0:1組卷：140引用：2難度：0.3