綜合與實踐：
動手操作：某校八（1）班數學課外興趣小組在學完第13章的特殊三角形后，利用手頭上的一副三角板，他們將一塊直角三角板DOE（DOE=90°，∠E=30°）的直角頂點O放置在另一塊直角三角板ABC（∠C=90°，AC=BC）斜邊AB的中點處，并將三角板DOE繞點O任意旋轉．
發現結論：
（1）如圖1，三角板DOE的兩邊DO，EO分別與另一塊三角板的邊AC，BC交于點P，Q（規定：此時點P，Q均在邊AC，BC上運動），他們在旋轉過程中，發現線段AP與CQ的長總相等及四邊形OPCQ的面積不會發生變化．
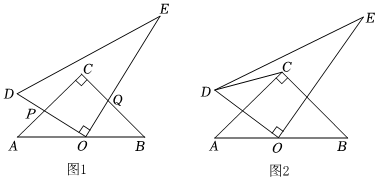
問題解決：①請你幫他們說明AP=CQ的理由；
②若AB=12cm,請你幫他們求出四邊形OPCQ的面積．
拓展延伸：
（2）如圖2，連接CD，當AB=12cm,DE=14cm時，那么直角三角板DOE在繞點O旋轉一周的過程中，請你直接寫出線段CD長的最小值和最大值．
【考點】四邊形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/1 8:0:9組卷：123引用：4難度：0.3
相似題
-
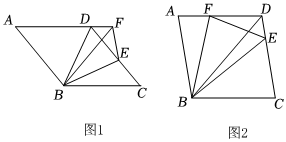1．如圖1，BD是菱形ABCD的對角線，點E是邊CD上一點，將△BCE沿著BE翻折，點C的對應點F恰好落在AD的延長線上，且AB=5．
（1）求證：FB平分∠AFE；
（2）如圖2，若點F落在AD上．
①猜想∠ABF與∠DBE之間的數量關系，并證明你的結論；
②若，求證：EC=3DE．DFFB=23發布：2025/6/9 14:30:1組卷：155引用：3難度：0.3 -
2．（1）如圖1，在四邊形ABCD中，∠ABC=∠ADC=90°，AD=CD，對角線BD=8，求四邊形ABCD的面積；
（2）如圖2，園藝設計師想在正六邊形草坪一角∠BOC內改建一個小型的兒童游樂場OMAN．其中OA平分∠BOC，OA=100米，∠BOC=120°，點M，N分別在射線OB和OC上，且∠MAN=90°，為了盡可能的少破壞草坪，要使游樂場OMAN面積最小，你認為園林規劃局的想法能實現嗎？若能，請求出游樂場OMAN面積的最小值；若不能，請說明理由．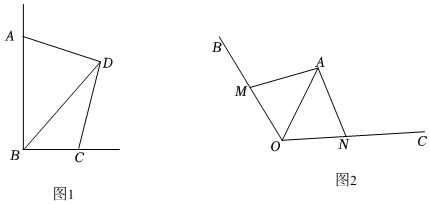
發布：2025/6/9 15:0:1組卷：243引用：2難度：0.2 -
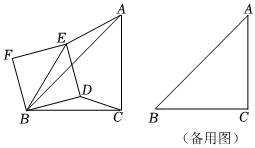3．如圖，在Rt△ABC中，AC=BC=4，∠ACB=90°，正方形BDEF的邊長為2，將正方形BDEF繞點B旋轉一周，連接AE、BE、CD．
（1）請判斷線段AE和CD的數量關系，并說明理由；
（2）當A、E、F三點在同一直線上時，求CD的長；
（3）設AE的中點為M，連接FM，試求線段FM長的取值范圍．發布：2025/6/9 15:0:1組卷：209引用：1難度：0.1