如圖，已知AB∥CD，現將一直角三角形PMN放入圖中，其中∠P=90°，PM交AB于點E，PN交CD于點F．
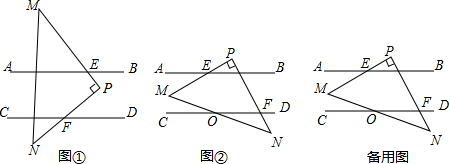
（1）當△PMN所放位置如圖①所示時，則∠PFD與∠AEM的數量關系為∠PFD+∠AEM=90°∠PFD+∠AEM=90°．請說明理由作PG∥AB，如圖①所示
則PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，作PG∥AB，如圖①所示
則PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，．
（2）當△PMN所放位置如圖②所示時，∠PFD與∠AEM的數量關系為∠PFD-∠AEM=90°∠PFD-∠AEM=90°．
（3）在（2）的條件下，若MN與CD交于點O，且∠DON=30°，∠PEB=15°，求∠N的度數．
則PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，
則PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，
【考點】平行線的性質．
【答案】∠PFD+∠AEM=90°；作PG∥AB，如圖①所示
則PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，；∠PFD-∠AEM=90°
則PG∥CD，
∴∠PFD=∠1，∠2=∠AEM，
∵∠1+∠2=∠P=90°，
∴∠PFD+∠AEM=∠1+∠2=90°，；∠PFD-∠AEM=90°
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：858引用：4難度：0.8
相似題
-
1．如圖，已知AB∥DE，∠ABC=70°，∠CDE=140°，則∠BCD=．發布：2025/6/8 21:0:2組卷：842引用：15難度：0.7 -
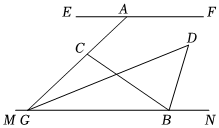2．如圖，直線EF∥MN，點A，B分別是EF，MN上的動點，點G在MN上，∠ACB=m°，∠AGB和∠CBN的角平分線交于點D，若∠D=50°，則m的值為（ ）發布：2025/6/8 21:30:1組卷：714引用：5難度：0.6 -
3．如圖，AB∥CD，點E為兩直線之間的一點．
（1）如圖1，若∠BAE=35°，∠DCE=20°，則∠AEC=（直接寫出結果即可）；
（2）如圖2，試說明，∠BAE+∠AEC+∠ECD=360°；
（3）如圖3，若∠BAE的平分線與∠DCE的平分線相交于點F，判斷∠AEC與∠AFC的數量關系，并說明理由．發布：2025/6/8 21:30:1組卷：213引用：3難度：0.5