某襯衣店將進價為30元的一種襯衣以40元售出，平均每月能售出600件，調查表明：這種襯衣售價每上漲1元，其銷售量將減少10件．
（1）求出月銷售利潤y（元）與售價x（元/件）之間的函數關系式；
（2）襯衣店想在月銷售量不少于300件的情況下，使月銷售利潤達到10000元，則售價應定為多少？
（3）當銷售價定為多少元時會獲得最大利潤？求出最大利潤．
【答案】（1）y=-10x2+1300x-30000；
（2）50元/件；
（3）當每件售價為65元時，可以獲得最大利潤為12250元．
（2）50元/件；
（3）當每件售價為65元時，可以獲得最大利潤為12250元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/8/20 18:0:1組卷：1298引用：5難度：0.5
相似題
-
1．小明同學利用寒假30天時間販賣草莓，了解到某品種草莓成本為10元/千克，在第x天的銷售量與銷售單價如下（每天內單價和銷售量保持一致）：
設第x天的利潤w元．銷售量m（千克） m=40-x 銷售單價n（元/千克） 當1≤x≤15時，n=20+ x12當16≤x≤30時，n=10+ 300x
（1）請計算第幾天該品種草莓的銷售單價為25元/千克？
（2）這30天中，該同學第幾天獲得的利潤最大？最大利潤是多少？注：利潤=（售價-成本）×銷售量
（3）在實際銷售的前15天中，草莓生產基地為刺激銷售，鼓勵銷售商批發草莓，每批發1千克就發給a（a≥2）元獎勵．通過銷售記錄發現，前8天中，每天獲得獎勵后的利潤隨時間x（天）的增大而增大，試求a的取值范圍．12發布：2025/6/18 3:0:1組卷：593引用：2難度：0.5 -
2．心理學家發現：學生對提出概念的接受能力y與提出概念的時間x（min）之間滿足二次函數關系y=-0.1x2+2.6x+43．則使學生對概念的接受能力最大．則提出概念的時間應為（ ）
發布：2025/6/18 3:30:2組卷：139引用：2難度：0.8 -
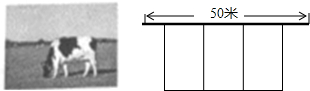3．某農場擬建三間長方形種牛飼養室，飼養室的一面靠墻（墻長50m），中間用兩道墻隔開（如圖）．已知計劃中的建筑材料可建墻的總長度為48m,則這三間長方形種牛飼養室的總占地面積的最大值為 m2．發布：2025/6/18 2:0:1組卷：4327引用：11難度：0.5