如圖（1）是一種簡易臺燈，在其結構圖（2）中燈座為△ABC（BC伸出部分不計），A、C、D在同一直線上．量得∠ACB=90°，∠A=60°，AB=16cm,∠ADE=135°，燈桿CD長為40cm,燈管DE長為15cm.
（1）求DE與水平桌面（AB所在直線）所成的角；
（2）求臺燈的高（點E到桌面的距離，結果精確到0.1cm）．
（參考數據：sin15°=0.26，cos15°=0.97，tan15°=0.27，sin30°=0.5，cos30°=0.87，tan30°=0.58．）
【考點】解直角三角形的應用．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/21 12:0:1組卷：3416引用：16難度：0.3
相似題
-
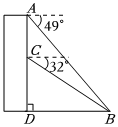1．如圖，小聰在一幢樓的樓頂A點處，以49°的俯角看到一盞路燈的底部B點，小輝在這幢樓的C點處，以32°的俯角看到這盞路燈的底部B點．路燈到樓的距離BD=20米，點A，C，D在同一直線上．已知sin49°=0.7547，cos49°=0.6561，tan49°=1.1504，sin32°=0.5299，cos32°=0.8481，tan32°=0.6249．則小聰和小輝所在測量位置之間的距離AC約為（ ）發布：2025/5/21 19:30:2組卷：323引用：3難度：0.5 -
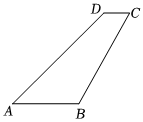2．如圖是某一個機器所需要的四邊形零件的圖形，它的具體參數如下：AB∥CD，∠D=135°，∠C=60°，CD=2cm,BC=8cm,求這個四邊形零件的邊AB和AD的長．（結果保留根號）發布：2025/5/21 19:30:2組卷：41引用：2難度：0.5 -
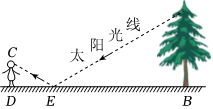3．為了測量校園水平地面上一棵不可攀爬的樹的高度，小明利用物理學中“光的反射定律”做了如下的探索：如圖，找一面很小的鏡子放在合適的位置（點E處），小明站在點D處剛好能在鏡子里看到樹梢頂點，此時小明看鏡子的視線與地面的夾角為30°（即∠CED=30°），鏡子到大樹的水平距離BE為30米，則樹的高度為 米（注：反射角等于入射角，結果若有根號則保留根號）．發布：2025/5/21 20:0:2組卷：104引用：2難度：0.7