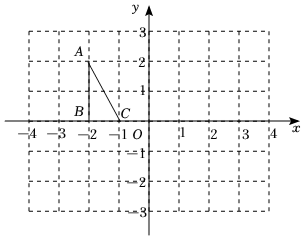
如圖，在直角坐標系中，邊長為1的小正方形組成的網格中，給出了格點△ABC（頂點為網格線的交點），在給定的網格中，解答下列問題：
（1）以A為位似中心，將△ABC按相似比2：1放大，得到△AB1C1，畫出△AB1C1．
（2）以C1為旋轉中心，將△AB1C1順時針旋轉90°，得到△A1B2C1．
①畫出△A1B2C1；
②求點A的運動路徑長．
【考點】相似形綜合題．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/1 16:30:1組卷：198引用：7難度：0.6
相似題
-
1．【教材呈現】如圖是華師版八年級上冊數學教材第96頁的部分內容．
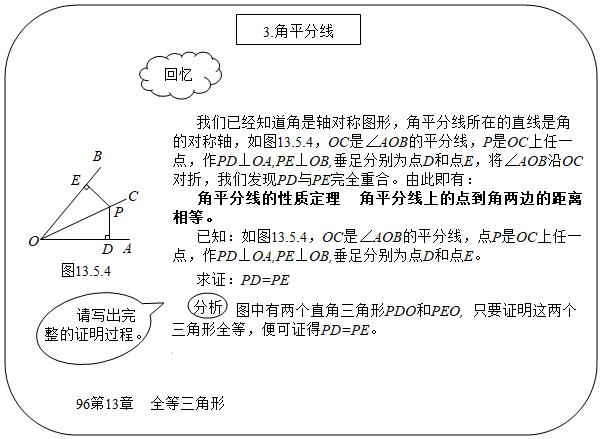
【定理證明】結合圖①，“角平分線的性質定理”證明過程中．運用了△ODP與△OEP全等，全等最直接的依據是 ；
【定理感知】如果教材中的已知條件不變，如圖①，當PD=3，OE=6時，則△OPE面積為 ；
【定理應用】如圖②，在△ABC中，AD平分∠BAC交BC于點D．求證：；BDDC=ABAC
【拓展應用】如圖③，在△ABC中，∠ABC=90°，AB=6，BC=8，將△ABC先沿∠BAC的平分線AB1折疊，再剪掉重疊部分（即四邊形ABB1A1），再將余下部分沿∠B1A1C的平分線A1B2折疊，再剪掉重疊部分，直接寫出剩余的△A2B2C的面積為 ．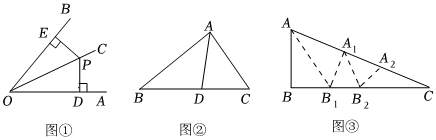
發布：2025/6/2 21:30:9組卷：170引用：1難度：0.1 -
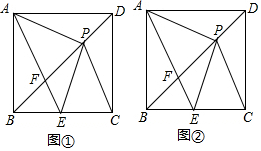2．如圖①，在正方形ABCD中，點E為BC邊的中點，P為對角線BD上的一點，連接AE交BD于點F，連接PA、PE、PC．
（1）求證：PA=PC；
（2）若PE=PC，求證：PE2=PF?PB；
（3）如圖②，若△ADP≌△ABF，AB=6，求PE的長．發布：2025/6/2 22:0:1組卷：766引用：3難度：0.3 -
3．在△EFG中，∠EFG=90°，EF=FG，且點E，F分別在矩形ABCD的邊AB，AD上，AB=8，AD=6．
（1）如圖1，當點G在CD上時，求AE+DG的值；
（2）如圖2，FG與CD相交于點N，連接EN，當EF平分∠AEN時，求證：EN=AE+DN；
（3）如圖3，EG，FG分別交CD于點M，N，當MG2=MN?MD時，求AE的值．發布：2025/6/2 22:30:1組卷：199引用：2難度：0.3