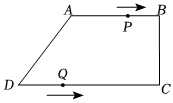
在四邊形ABCD中，AB∥CD，∠BCD=90°，AB=AD=10cm,BC=8cm,點P從點A出發，沿折線ABCD方向以3cm/s的速度勻速運動；點Q從點D出發，沿線段DC方向以2cm/s的速度勻速運動．已知兩點同時出發，當一個點到達終點時，另一點也停止運動，設運動時間為t（s）．
（1）求CD的長；
（2）當四邊形PBQD為平行四邊形時，求四邊形PBQD的周長；
（3）在點P、Q的運動過程中，是否存在某一時刻，使得△BPQ的面積為16cm2？若存在，請求出所有滿足條件的t的值；若不存在，請說明理由．
【考點】四邊形綜合題．
【答案】（1）CD的長為16cm；
（2）四邊形PBQD的周長為
（3）存在，當t的值為2或或6時，△BPQ的面積為16cm2．
（2）四邊形PBQD的周長為
（
8
+
8
13
）
cm
（3）存在，當t的值為2或
16
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：131引用：3難度：0.1
相似題
-
1．定義：我們把對角線相等的四邊形叫做和美四邊形．
（1）請舉出一種你所學過的特殊四邊形中是和美四邊形的例子．
（2）如圖1，E，F，G，H分別是四邊形ABCD的邊AB，BC，CD，DA的中點，已知四邊形EFGH是菱形，求證：四邊形ABCD是和美四邊形；
（3）如圖2，四邊形ABCD是和美四邊形，對角線AC，BD相交于O，∠AOB=60°，E、F分別是AD、BC的中點，請探索EF與AC之間的數量關系，并證明你的結論．
發布：2025/6/5 3:0:1組卷：914引用：7難度：0.3 -
2．如圖1，圖2，在?ABCD中，AB為定值，BC=2x（x＞0），∠ABC和∠BCD的平分線BE與CF交于點G，點E，F在直線AD上，線段EF的長為y,圖3是y與x的函數圖象．
（1）①線段AE與線段DF的關系是：AE DF（填“＜”，“＞”或“=”）；
②線段AB長為 ；圖3中a的值是 ；
（2）當點F在線段AE延長線上時，求y與x的函數關系式并寫出自變量x的取值范圍；
（3）線段AE延長線上有點P，PE=m?BC，填空：
①若m=，則當x為 時，P，F兩點重合；12
②若要使4≤x≤8時，P，F兩點能夠重合，則m的最大值是 ．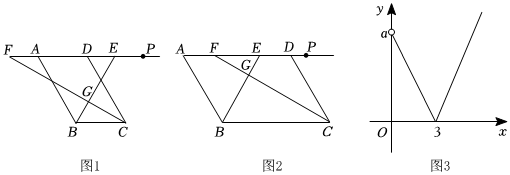
發布：2025/6/5 3:0:1組卷：83引用：2難度：0.4 -
3．綜合與實踐：折紙中的數學
知識初探：
（1）如圖1，長方形紙條ABGH中，AB∥GH，AH∥BG，∠A=∠B=∠G=∠H=90°，將長方形紙條沿直線CD折疊，點A落在A′處，點B落在B′處，B′C交AH于點E，若∠ECG=50°，則∠CDE=；
類比再探：
（2）如圖2，在圖1的基礎上將∠HEC對折，點H落在直線EC上的H′處，點G落在G′處得到折痕EF，則折痕EF與CD有怎樣的位置關系？并說明理由；
拓展延伸：
（3）如圖3，在圖2的基礎上，過點G′作BG的平行線MN，請你猜想∠ECF與∠H′G′M的數量關系，并說明理由．
發布：2025/6/5 3:0:1組卷：148引用：1難度：0.3