隨機變量的概念是俄國數學家切比雪夫在十九世紀中葉建立和提倡使用的.切比雪夫在數論、概率論、函數逼近論、積分學等方面均有所建樹,他證明了如下以他名字命名的離散型切比雪夫不等式:設X為離散型隨機變量,則P(|X-E(X)|≥λ)≤D(X)λ2,其中λ為任意大于0的實數.切比雪夫不等式可以使人們在隨機變量X的分布未知的情況下,對事件|X-λ|≤λ的概率作出估計.
(1)證明離散型切比雪夫不等式;
(2)應用以上結論,回答下面問題:
已知正整數n≥5.在一次抽獎游戲中,有n個不透明的箱子依次編號為1,2,?,n,編號為i(1≤i≤n)的箱子中裝有編號為0,1,?,i的i+1個大小、質地均相同的小球.主持人邀請n位嘉賓從每個箱子中隨機抽取一個球,記從編號為i的箱子中抽取的小球號碼為Xi,并記X=n∑i=1Xii.對任意的n,是否總能保證P(X≤0.1n)≥0.01(假設嘉賓和箱子數能任意多)?并證明你的結論.
附:可能用到的公式(數學期望的線性性質):
對于離散型隨機變量X,X1,X2,?,Xn滿足X=n∑i=1Xi,則有E(X)=n∑i=1E(Xi).
D
(
X
)
λ
2
n
∑
i
=
1
X
i
i
n
∑
i
=
1
X
i
n
∑
i
=
1
E
(
X
i
)
【考點】離散型隨機變量的均值(數學期望).
【答案】(1)證明見解析;
(2)不能保證P(X≤0.1n)≥0.01,證明見解析.
(2)不能保證P(X≤0.1n)≥0.01,證明見解析.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:172引用:2難度:0.6
相似題
-
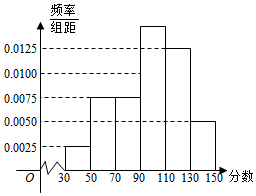 1.某市舉行“中學生詩詞大賽”,分初賽和復賽兩個階段進行,規定:初賽成績大于90分的具有復賽資格,某校有800名學生參加了初賽,所有學生的成績均在區間(30,150]內,其頻率分布直方圖如圖.
1.某市舉行“中學生詩詞大賽”,分初賽和復賽兩個階段進行,規定:初賽成績大于90分的具有復賽資格,某校有800名學生參加了初賽,所有學生的成績均在區間(30,150]內,其頻率分布直方圖如圖.
(Ⅰ)求獲得復賽資格的人數;
(Ⅱ)從初賽得分在區間(110,150]的參賽者中,利用分層抽樣的方法隨機抽取7人參加學校座談交流,那么從得分在區間(110,130]與(130,150]各抽取多少人?
(Ⅲ)從(Ⅱ)抽取的7人中,選出3人參加全市座談交流,設X表示得分在區間(130,150]中參加全市座談交流的人數,求X的分布列及數學期望E(X).發布:2024/12/29 13:30:1組卷:134引用:7難度:0.5 -
2.設離散型隨機變量X的分布列如表:
若離散型隨機變量Y=-3X+1,且E(X)=3,則( )X 1 2 3 4 5 P m 0.1 0.2 n 0.3 A.m=0.1 B.n=0.1 C.E(Y)=-8 D.D(Y)=-7.8 發布:2024/12/29 13:0:1組卷:199引用:6難度:0.5 -
3.從4名男生和2名女生中任選3人參加演講比賽,用X表示所選3人中女生的人數,則E(X)為( )
A.0 B.1 C.2 D.3 發布:2024/12/29 13:30:1組卷:139引用:6難度:0.7


