2016年第二十一屆華羅庚金杯少年數(shù)學(xué)邀請(qǐng)賽決賽數(shù)學(xué)試卷（初一組）

一、填空題（共8小題，每小題8分，滿分64分）

• 1．已知n個(gè)數(shù)x₁，x₂，…，x_n，每個(gè)數(shù)只能取0，1，-1中的一個(gè)，若x₁+x₂+…+x_n=2016，則x₁²⁰¹⁵+x₂²⁰¹⁵+…+x_n²⁰¹⁵的值為

   

  ．
  組卷：291引用：2難度：0.5

  解析

• 2．某停車場(chǎng)白天和夜間兩個(gè)不同時(shí)段的停車費(fèi)用的單價(jià)不同，張明2月份白天的停車時(shí)間比夜間要多40%，3月份白天的停車時(shí)間比夜間要少40%．若3月份的總停車時(shí)間比2月份多20%，但停車費(fèi)用卻少了20%，那么該停車場(chǎng)白天時(shí)段與夜間時(shí)段停車費(fèi)用的單價(jià)之比是

  ．
  組卷：77引用：2難度：0.8

  解析

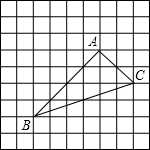• 3．在9×9的格子紙上，1×1小方格的頂點(diǎn)叫做格點(diǎn)．如圖，三角形ABC的三個(gè)頂點(diǎn)都是格點(diǎn)．若一個(gè)格點(diǎn)P使得三角形PAB與三角形PAC的面積相等，就稱P點(diǎn)為“好點(diǎn)”，那么在這張格子紙上共有

  個(gè)“好點(diǎn)”．
  組卷：119引用：2難度：0.4

  解析

• 4．設(shè)正整數(shù)x,y滿足xy-9x-9y=20，則x²+y²=

  ．
  組卷：156引用：1難度：0.4

  解析

二、解答題（共6小題，滿分70分）

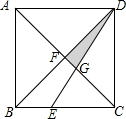• 13．如圖，四邊形ABCD是正方形，F(xiàn)是其兩條對(duì)角線的交點(diǎn)，E在BC邊上，BE：EC=1：2，DE與對(duì)角線AC的交點(diǎn)為G，三角形DFG的面積等于2，求正方形ABCD的面積．
  組卷：188引用：1難度：0.5

  解析

• 14．排成一行的學(xué)生，從左到右1至3報(bào)數(shù)，最后一個(gè)人報(bào)2，從右到左1至m報(bào)數(shù)，最后一個(gè)人報(bào)1，這里m與3互質(zhì)．現(xiàn)凡報(bào)過1的學(xué)生出列，其余原地不動(dòng)，共留下62名，其中只有21對(duì)學(xué)生原來(lái)相鄰，問原來(lái)有多少名學(xué)生？m的值是多少？
  組卷：71引用：1難度：0.3

  解析