2017-2018學(xué)年重慶市九龍坡區(qū)育才中學(xué)九年級（上）第一次月考數(shù)學(xué)試卷

一、選擇題：（本大題共12個小題，每小題4分，共48分）在每個小題的下面，都給出了代號為A、B、C、D的四個答案，其中只有一個是正確的，請將答題卡上題號右側(cè)正確答案所對應(yīng)的方框涂黑．

• 1．在實(shí)數(shù)-3，-2，0，-4中，最小的數(shù)是（　　）

  A．-3

  B．2

  C．0

  D．-4
  組卷：8引用：2難度：0.9

  解析

• 2．下列圖形中，是軸對稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：1404引用：246難度：0.9

  解析

• 3．計(jì)算（-2x³y）²的結(jié)果是（　　）

  A．4x5y2

  B．-4x5y2

  C．4x6y2

  D．-4x6y2
  組卷：305引用：7難度：0.9

  解析

• 4．下列調(diào)查中，最適合采用全面調(diào)查（普查）方式的是（　　）

  A．對某批節(jié)能點(diǎn)燈的使用壽命的調(diào)查

  B．對重慶市初三學(xué)生每天的體育鍛煉時(shí)間的調(diào)查

  C．對某校九年級3班學(xué)生一周使用手機(jī)時(shí)間的調(diào)查

  D．對中秋節(jié)期間市場上某品牌月餅在我市銷售情況的調(diào)查
  組卷：9引用：2難度：0.9

  解析

• 5．估計(jì)

  7

  -

  1

  2

  的值應(yīng)在（　　）

  A．0.70和0.75之間	B．0.75和0.80之間
  C．0.80和0.85之間	D．0.85和0.90之間
  組卷：21引用：2難度：0.9

  解析

• 6．若y=-

  1

  3

  是關(guān)于的方程2x-3y=-3的解，則x值為（　　）

  A．-2

  B．- 11 9

  C．-1

  D． 7 9
  組卷：35引用：1難度：0.7

  解析

• 7．要使分式

  x

  +

  4

  x

  -

  3

  有意義，x應(yīng)滿足的條件是（　　）

  A．x＞3

  B．x＞3且x≠4

  C．x≥3

  D．x≥3且x≠4
  組卷：108引用：1難度：0.9

  解析

• 8．△ABC∽△DEF，且它們的周長之比為2：3，則它們的面積之比為（　　）

  A．2：3

  B．4：6

  C．4：9

  D．3：2
  組卷：45引用：3難度：0.7

  解析

五、解答題：（本大題2個小題，第25小題10分，第26小題12分，共22分）解答時(shí)每小題必須給出必要的演算過程或推理步驟，請將解答過程書寫在答題卡中對應(yīng)的位置上．

• 25．對任意一個三位數(shù)P，將它任意兩個數(shù)位上的數(shù)字對調(diào)后得到一個首位不為0的新的三位數(shù)q（q可以與P相同），記q=

  abc

  ，在所有可能的情況中，當(dāng)|a-2b+c|最小時(shí)，我們稱此時(shí)的q是p“幸福快樂數(shù)”，并規(guī)定：K（p）=a²-2b²+c²．例如：318按上述方法可得新數(shù)有381、813、138，因?yàn)閨3-2×8+1|=12，|8-2×1+3|=9，|1-2×3+8|=3，而3＜9＜12，所以138是318的“幸福快樂數(shù)”，
  此時(shí)K（318）=1²-2×3²+8²=47．
  （1）計(jì)算：K（168），K（243）：
  （2）若m=100x+10y+8（1≤x≤y≤9，x、y都是正整數(shù)），交換其十位與百位上的數(shù)字得到新數(shù)n,若m+n是13的倍數(shù)時(shí)，求K（n）的最大值．
  組卷：410引用：2難度：0.6

  解析

• 26．如圖1，二次函數(shù)y=ax²-2x+c（a≠0）的圖象交x軸于點(diǎn)A（-1，0）、B（3，0）兩點(diǎn)，與y軸交于點(diǎn)C，點(diǎn)D是拋物線的頂點(diǎn)，DH⊥x軸于點(diǎn)H連接AC，BC．
  （1）求拋物線的解析式；
  （2）如圖2，點(diǎn)P是拋物線第一象限上一點(diǎn)，且滿足△PBC的面積等于△ABC的面積．
  ①求點(diǎn)P的坐標(biāo)；②點(diǎn)Q與點(diǎn)C關(guān)于直線DH對稱，在x軸上找一點(diǎn)E，使得|EP-EQ|的值最大，求點(diǎn)E坐標(biāo)以及這個最大值；
  （3）如圖3，在（2）問的條件下，設(shè)直線PE交y軸于點(diǎn)G，交直線DH于點(diǎn)F，y軸上有一定點(diǎn)M（0，4），點(diǎn)K為PQ的中點(diǎn)，連接MF，先將△MFG沿著直線MF翻折到△MFN，再將拋物線y=ax²-2x+c沿著其對稱軸DH向上平移，得到拋物線y₁，使得拋物線y₁的圖象剛好過點(diǎn)N，此時(shí)拋物線y₁交y軸于點(diǎn)T，連接TK．請問在直線PE上是否存在一點(diǎn)Y，使得△TKY是直角三角形？若存在，請直接寫出點(diǎn)Y的坐標(biāo)；若不存在，請說明理由．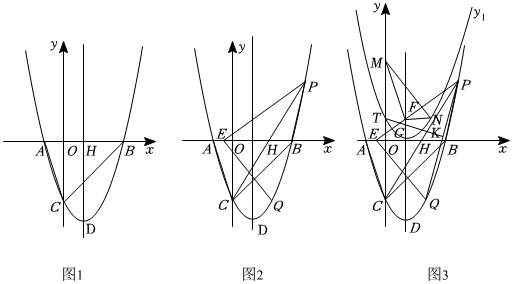
  組卷：41引用：1難度：0.2

  解析