《圓錐曲線與方程》2013年高三數學一輪復習單元訓練（北京郵電大學附中）

一、選擇題（本大題共12個小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項是符合題目要求的）

• 1．雙曲線

  x

  2

  12

  -

  y

  2

  4

  =

  1

  的漸近線方程為（　　）

  A． 2 x ± y = 0

  B． x ± 2 y = 0

  C． 3 x ± y = 0

  D． x ± 3 y = 0
  組卷：20引用：6難度：0.9

  解析

• 2．在同一坐標系中，方程a²x²+b²y²=1與ax+by²=0（a＞b＞0）的曲線大致是（　　）

  A．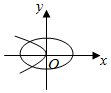

  B．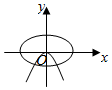

  C．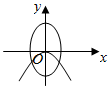

  D．
  組卷：1023引用：62難度：0.9

  解析

• 3．已知P是橢圓

  x

  2

  5

  +

  y

  2

  4

  =

  1

  上一點，F₁和F₂是焦點，若∠F₁PF₂=30°，則△PF₁F₂的面積為（　　）

  A． 4 3 3

  B． 4 （ 2 - 3 ）

  C．4（2+ 3 ）

  D．4
  組卷：172引用：13難度：0.9

  解析

• 4．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的兩條漸近線均和圓C：x²+y²-6x+5=0相切，且雙曲線的右焦點為圓C的圓心，則該雙曲線的方程為（　　）

  A． x 2 5 - y 2 4 =1

  B． x 2 4 - y 2 5 =1

  C． x 2 3 - y 2 6 =1

  D． x 2 6 - y 2 3 =1
  組卷：998引用：59難度：0.7

  解析

• 5．已知F是橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的左焦點，P是橢圓上的一點，PF⊥x軸，OP∥AB（O為原點），則該橢圓的離心率是（　　）

  A． 2 2

  B． 2 4

  C． 1 2

  D． 3 2
  組卷：196引用：22難度：0.9

  解析

• 6．經過原點且與拋物線y=（x+1）²-

  3

  4

  只有一個公共點的直線有多少條？（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：37引用：1難度：0.5

  解析

• 7．若點O和點F（-2，0）分別是雙曲線

  x

  2

  a

  2

  -y²=1（a＞0）的中心和左焦點，點P為雙曲線右支上的一點，并且P點與右焦點F′的連線垂直x軸，則線段OP的長為（　　）

  A． 13 3

  B． 39 3

  C． 7 3

  D． 21 3
  組卷：36引用：4難度：0.7

  解析

三、解答題（本大題共6個小題，共70分，解答應寫出文字說明，證明過程或演算步驟）

• 20．設F₁，F₂分別為橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0）的左、右焦點，過F₂的直線l與橢圓C相交于A，B兩點，直線l的傾斜角為60°，F₁到直線l的距離為

  2

  3

  ．
  （Ⅰ）求橢圓C的焦距；
  （Ⅱ）如果

  A

  F

  2

  =

  2

  F

  2

  B

  ，求橢圓C的方程．
  組卷：1696引用：24難度：0.5

  解析

• 21．設拋物線C：x²=2py（p＞0）的焦點為F，A（x₀，y₀）（x₀≠0）是拋物線C上的一定點．
  （1）已知直線l過拋物線C的焦點F，且與C的對稱軸垂直，l與C交于Q，R兩點，S為C的準線上一點，若△QRS的面積為4，求p的值；
  （2）過點A作傾斜角互補的兩條直線AM，AN，與拋物線C的交點分別為M（x₁，y₁），N（x₂，y₂）．若直線AM，AN的斜率都存在，證明：直線MN的斜率等于拋物線C在點A關于對稱軸的對稱點A₁處的切線的斜率．
  組卷：30引用：3難度：0.5

  解析