2020-2021學年山東省青島市市南區九年級（下）期初數學試卷

一．選擇題（共8小題）

• 1．如圖所示的紫砂壺，其俯視圖是（　　）

  A．

  B．

  C．

  D．
  組卷：64引用：2難度：0.9

  解析

• 2．關于x的方程（m-2）x²+2x+1=0有實數根，則m的取值范圍是（　　）

  A．m≤3

  B．m≥3

  C．m≤3且m≠2

  D．m＜3
  組卷：2158引用：11難度：0.7

  解析

• 3．學校圖書館去年年底有圖書5萬冊，預計到明年年底增加到7.2萬冊．設這兩年的平均增長率為x,則下列方程正確的是（　　）

  A．5（1+x）=7.2	B．5（1+2x）=7.2
  C．5（1+x）2=7.2	D．5（1+x）+5（1+x）2=7.2
  組卷：40引用：9難度：0.9

  解析

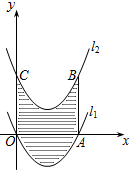• 4．如圖，已知拋物線l₁：y=（x-2）²-4與x軸分別交于O、A兩點，將拋物線l₁向上平移得到l₂，過點A作AB⊥x軸交拋物線l₂于點B，如果由拋物線l₁、l₂、直線AB及y軸所圍成的陰影部分的面積為12，則拋物線l₂的函數表達式為（　　）

  A．y=（x-2）2-1

  B．y=（x-2）2+1

  C．y=（x-2）2-2

  D．y=（x-2）2+2
  組卷：651引用：4難度：0.5

  解析

• 5．籠子里關著一只小松鼠（如圖），籠子主人決定把小松鼠放歸大自然，將籠子所有的門都打開，松鼠要先過第一道門（A或B），再過第二道門（C，D或E）才能出去，則松鼠走出籠子的路線（經過的兩道門）的不同可能有（　　）

  A．2種

  B．3種

  C．5種

  D．6種
  組卷：219引用：3難度：0.5

  解析

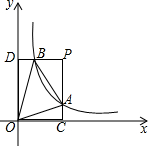• 6．如圖，過點P（2，3）分別作PC⊥x軸于點C，PD⊥y軸于點D，PC，PD分別交反比例函數y=

  k

  x

  （x＞0）的圖象于點A，B，△OAB的面積為

  8

  3

  ，則k的值是（　　）

  A．2

  B． 2 2 3

  C． 8 3

  D．3
  組卷：1567引用：2難度：0.7

  解析

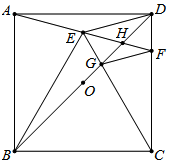• 7．如圖，正方形ABCD中，O為BD中點，以BC為邊向正方形內作等邊△BCE，連接并延長AE交CD于F，連接BD分別交CE，AF于G，H，下列結論：①∠CEH=45°；②GF∥DE；③2OH+DH=BD；④BG=

  2

  DG；⑤S_△BEC：S_△BGC=

  3

  +

  1

  2

  ．其中正確的結論是（　　）

  A．①②⑤

  B．①②④

  C．①②

  D．②③④
  組卷：1102引用：6難度：0.4

  解析

• 8．已知a,b是非零實數，|b|＞|a|，在同一平面直角坐標系xOy中，二次函數y₁=ax²-bx與一次函數y₂=ax-b的大致圖象不大可能的是（　　）

  A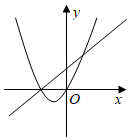．	B．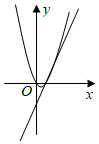
  C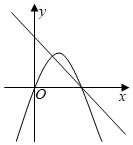．	D．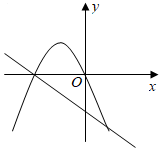
  組卷：910引用：3難度：0.6

  解析

三．作圖題不寫作法，保留作圖痕跡（4分）

• 23．問題提出：已知矩形ABCD，點E為AB上的一點，EF⊥AB，交BD于點F．將△EBF繞點B順時針旋轉α（0°＜α＜90°）得到△E'BF'，則AE'與DF'的有怎樣的數量關系．
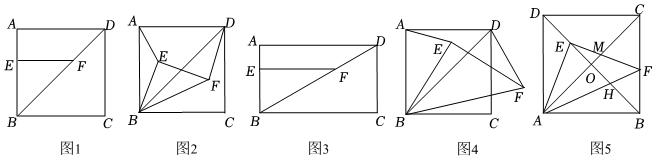
  問題探究
  探究一：如圖，已知正方形ABCD，點E為AB上的一點，EF⊥AB，交BD于點F．
  （1）如圖1，直接寫出

  DF

  AE

  的值

  ；
  （2）將△EBF繞點B順時針旋轉到如圖2所示的位置，連接AE、DF，猜想DF與AE的數量關系，并證明你的結論；
  探究二：如圖，已知矩形ABCD，點E為AB上的一點，EF⊥AB，交BD于點F．
  如圖3，若四邊形ABCD為矩形，

  AB

  BC

  =

  2

  2

  ，將△EBF繞點B順時針旋轉α（0^o＜α≤90^o）得到△E'BF'（E、F的對應點分別為E'、F'點），連接AE'、DF'，則

  AE

  ′

  DF

  ′

  的值是否隨著α的變化而變化．若變化，請說明變化情況；若不變，請求出

  AE

  ′

  DF

  ′

  的值．
  一般規律
  如圖3，若四邊形ABCD為矩形，BC=mAB，其它條件都不變，將△EBF繞點B順時針旋轉α（0°＜α＜90°）得到△E'BF'，連接AE'，DF'，請直接寫出AE'與DF'的數量關系．
  問題解決
  如圖4，當BE=BA時，其他條件不變，△EBF繞點B順時針旋轉，設旋轉角為α（0°＜α＜360°）當EA=ED時，直接寫出此時α=

  ．
  拓展延伸
  如圖5，點E是正方形ABCD對角線BD上一點，連接AE，過點E作EF⊥AE，交線段BC于點F，交線段AC于點M，連接AF交線段BD于點H．給出下列四個結論，①AE=EF；②

  2

  DE=CF；③S_△AEM=S_△MCF；④BE=DE+

  2

  BF；正確的結論有

  個．
  組卷：657引用：3難度：0.3

  解析

• 24．如圖1，在Rt△ABC中，AB=AC=4

  2

  ，一動點P從點B出發，沿BC方向以每秒1個單位長度的速度勻速運動，到達點C即停止．在整個運動過程中，過點P作PD⊥BC與Rt△ABC的直角邊相交于點D，延長PD至點Q，使得PD=QD，以PQ為斜邊在PQ左側作等腰直角三角形PQE．設運動時間為t秒（t＞0）．解答下列問題：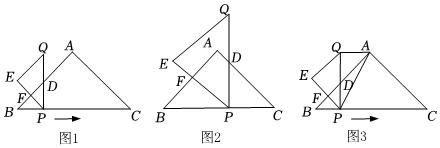
  （1）如圖2，求當t是多少時，點D與點A重合；
  （2）當t=

  16

  3

  時，點E在邊AB上，請求出當4＜t≤

  16

  3

  時，△ABC與△PQE重疊部分的面積的最大值；
  （3）是否存在某一時刻t,使得點E、D、C在同一直線上；如果存在，請求出t的值；如果不存在，請說明理由；
  （4）如圖3，當點D在線段AB上時，連接AQ，AP，是否存在這樣的t,使得△APQ成為等腰三角形？若存在，求出對應的t的值，若不存在，請說明理由．
  組卷：38引用：1難度：0.2

  解析