人教五四新版七年級（下）中考題單元試卷：第18章 全等三角形（08）

一、選擇題（共5小題）

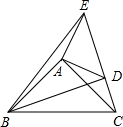• 1．已知：如圖在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，點C，D，E三點在同一條直線上，連接BD，BE．以下四個結論：
  ①BD=CE；
  ②BD⊥CE；
  ③∠ACE+∠DBC=45°；
  ④BE²=2（AD²+AB²），
  其中結論正確的個數是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：2633引用：91難度：0.7

  解析

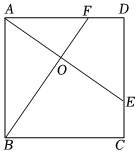• 2．如圖，E、F分別是正方形ABCD的邊CD、AD上的點，且CE=DF，AE、BF相交于點O，下列結論：（1）AE=BF；（2）AE⊥BF；（3）AO=OE；（4）S_△AOB=S_{四邊形DEOF}中正確的有（　　）

  A．4個

  B．3個

  C．2個

  D．1個
  組卷：3225引用：138難度：0.7

  解析

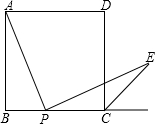• 3．如圖，已知邊長為4的正方形ABCD，P是BC邊上一動點（與B、C不重合），連接AP，作PE⊥AP交∠BCD的外角平分線于E．設BP=x,△PCE面積為y,則y與x的函數關系式是（　　）

  A．y=2x+1

  B．y= 1 2 x-2x2

  C．y=2x- 1 2 x2

  D．y=2x
  組卷：1008引用：59難度：0.9

  解析

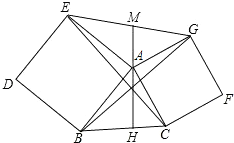• 4．在銳角三角形ABC中，AH是BC邊上的高，分別以AB、AC為一邊，向外作正方形ABDE和ACFG，連接CE、BG和EG，EG與HA的延長線交于點M，下列結論：①BG=CE； ②BG⊥CE； ③AM是△AEG的中線； ④∠EAM=∠ABC，其中正確結論的個數是（　　）

  A．4個

  B．3個

  C．2個

  D．1個
  組卷：3708引用：88難度：0.5

  解析

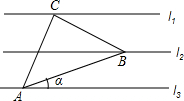• 5．如圖，已知l₁∥l₂∥l₃，相鄰兩條平行直線間的距離相等，等腰直角△ABC中，∠ACB=90°，三角形的三個頂點分別在這三條平行直線上，則sinα的值是（　　）

  A． 1 3

  B． 6 17

  C． 5 5

  D． 10 10
  組卷：2760引用：69難度：0.5

  解析

二、填空題（共3小題）

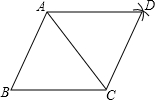• 6．如圖，以△ABC的頂點A為圓心，以BC長為半徑作弧；再以頂點C為圓心，以AB長為半徑作弧，兩弧交于點D；連接AD、CD．若∠B=65°，則∠ADC的大小為

  度．
  組卷：1424引用：92難度：0.7

  解析

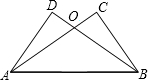• 7．如圖，已知∠C=∠D，∠ABC=∠BAD，AC與BD相交于點O，請寫出圖中一組相等的線段

  ．
  組卷：569引用：74難度：0.7

  解析

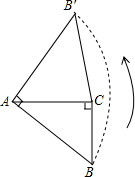• 8．如圖，Rt△ABC中，∠ACB=90°，AC=4，將斜邊AB繞點A逆時針旋轉90°至AB′，連接B′C，則△AB′C的面積為

  ．
  組卷：494引用：61難度：0.7

  解析

三、解答題（共22小題）

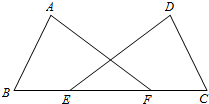• 9．如圖，點E、F在BC上，BE=FC，AB=DC，∠B=∠C．求證：∠A=∠D．
  組卷：7912引用：224難度：0.7

  解析

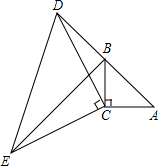• 10．如圖，在△ABC中，∠ACB=90°，AC=BC，延長AB至點D，使DB=AB，連接CD，以CD為直角邊作等腰三角形CDE，其中∠DCE=90°，連接BE．
  （1）求證：△ACD≌△BCE；
  （2）若AC=3cm,則BE=

   

  cm.
  組卷：1433引用：79難度：0.7

  解析

三、解答題（共22小題）

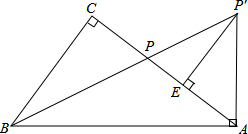• 29．如圖，在Rt△ABC中，∠C=90°，點P為AC邊上的一點，將線段AP繞點A順時針方向旋轉（點P對應點P′），當AP旋轉至AP′⊥AB時，點B、P、P′恰好在同一直線上，此時作P′E⊥AC于點E．
  （1）求證：∠CBP=∠ABP；
  （2）求證：AE=CP；
  （3）當

  CP

  PE

  =

  3

  2

  ，BP′=5

  5

  時，求線段AB的長．
  組卷：2039引用：68難度：0.1

  解析

• 30．正方形ABCD中，點E、F分別是邊AD、AB的中點，連接EF．
  （1）如圖1，若點G是邊BC的中點，連接FG，則EF與FG關系為：

  ；
  （2）如圖2，若點P為BC延長線上一動點，連接FP，將線段FP以點F為旋轉中心，逆時針旋轉90°，得到線段FQ，連接EQ，請猜想BF、EQ、BP三者之間的數量關系，并證明你的結論．
  （3）若點P為CB延長線上一動點，按照（2）中的作法，在圖3中補全圖形，并直接寫出BF、EQ、BP三者之間的數量關系：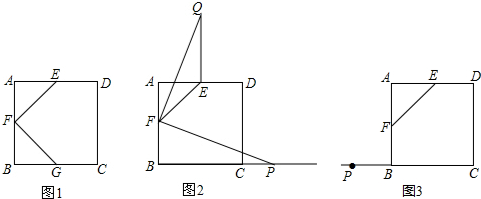

  ．
  
  組卷：1281引用：62難度：0.3

  解析