2022-2023學年山東省德州市禹城市、高新區八年級（下）期末數學試卷

一.單選題（48分）

• 1．下列運算正確的是（　　）

  A． 3 - 8 =2	B． a + 1 a - 1 a =a（a≠0）
  C． 5 + 5 = 10	D．a2?a3=a5
  組卷：1107引用：8難度：0.9

  解析

• 2．已知實數x,y滿足|x-4|

  +

  y

  -

  8

  =

  0

  ，則以x,y的值為兩邊長的等腰三角形的周長是（　　）

  A．20或16	B．20
  C．16	D．以上答案均不對
  組卷：5328引用：87難度：0.5

  解析

• 3．定義新運算“※”：對于實數m,n,p,q.有[m,p]※[q,n]=mn+pq,其中等式右邊是通常的加法和乘法運算，例如：[2，3]※[4，5]=2×5+3×4=22．若關于x的方程[x²+1，x]※[5-2k,k]=0有兩個實數根，則k的取值范圍是（　　）

  A．k＜ 5 4 且k≠0

  B．k ≤ 5 4

  C．k ≤ 5 4 且k≠0

  D．k≥ 5 4
  組卷：1833引用：18難度：0.6

  解析

• 4．如圖，在Rt△ABC中，∠ACB=90°，CE是斜邊AB上的中線，過點E作EF⊥AB交AC于點F．若BC=4，△AEF的面積為5，則sin∠CEF的值為（　　）

  A． 3 5

  B． 5 5

  C． 4 5

  D． 2 5 5
  組卷：7175引用：21難度：0.3

  解析

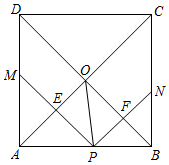• 5．如圖，在正方形ABCD中，點P是AB上一動點（不與A、B重合），對角線AC、BD相交于點O，過點P分別作AC、BD的垂線，分別交AC、BD于點E、F，交AD、BC于點M、N．下列結論：
  ①△APE≌△AME；
  ②PM+PN=AC；
  ③PE²+PF²=PO²；
  ④△POF∽△BNF；
  ⑤點O在M、N兩點的連線上．
  其中正確的是（　　）

  A．①②③④

  B．①②③⑤

  C．①②③④⑤

  D．③④⑤
  組卷：4543引用：23難度：0.3

  解析

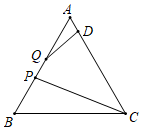• 6．如圖，等邊△ABC的邊長為3，點D在邊AC上，AD=

  1

  2

  ，線段PQ在邊BA上運動，PQ=

  1

  2

  ，有下列結論：
  ①CP與QD可能相等；
  ②△AQD與△BCP可能相似；
  ③四邊形PCDQ面積的最大值為

  31

  3

  16

  ；
  ④四邊形PCDQ周長的最小值為3+

  37

  2

  ．
  其中，正確結論的序號為（　　）

  A．①④

  B．②④

  C．①③

  D．②③
  組卷：4428引用：9難度：0.2

  解析

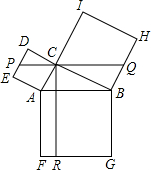• 7．如圖，在Rt△ABC中，∠ACB=90°，以其三邊為邊向外作正方形，過點C作CR⊥FG于點R，再過點C作PQ⊥CR分別交邊DE，BH于點P，Q．若QH=2PE，PQ=15，則CR的長為（　　）

  A．14

  B．15

  C．8 3

  D．6 5
  組卷：5709引用：18難度：0.2

  解析

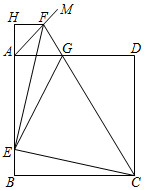• 8．如圖，正方形ABCD的邊長為4，點E在邊AB上，BE=1，∠DAM=45°，點F在射線AM上，且AF=

  2

  ，過點F作AD的平行線交BA的延長線于點H，CF與AD相交于點G，連接EC、EG、EF．下列結論：①△ECF的面積為

  17

  2

  ；②△AEG的周長為8；③EG²=DG²+BE²；其中正確的是（　　）

  A．①②③

  B．①③

  C．①②

  D．②③
  組卷：3369引用：9難度：0.3

  解析

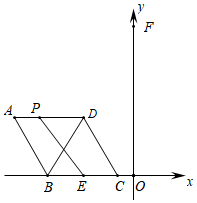• 9．如圖，菱形ABCD的頂點B、C在x軸上（B在C的左側），頂點A、D在x軸上方，對角線BD的長是

  2

  3

  10

  ，點E（-2，0）為BC的中點，點P在菱形ABCD的邊上運動．當點F（0，6）到EP所在直線的距離取得最大值時，點P恰好落在AB的中點處，則菱形ABCD的邊長等于（　　）

  A． 10 3

  B． 10

  C． 16 3

  D．3
  組卷：4557引用：10難度：0.1

  解析

四.解答題（72分）

• 27．如圖①，甲、乙都是高為6米的長方體容器，容器甲的底面ABCD是正方形，容器乙的底面EFGH是矩形．如圖②，已知正方形ABCD與矩形EFGH滿足如下條件：正方形ABCD外切于一個半徑為5米的圓O，矩形EFGH內接于這個圓O，EF=2EH．
  （1）求容器甲、乙的容積分別為多少立方米？
  （2）現在我們分別向容器甲、乙同時持續注水（注水前兩個容器是空的），一開始注水流量均為25立方米/小時，4小時后，把容器甲的注水流量增加a立方米/小時，同時保持容器乙的注水流量不變，繼續注水2小時后，把容器甲的注水流量再一次增加50立方米/小時，同時容器乙的注水流量仍舊保持不變，直到兩個容器的水位高度相同，停止注水．在整個注水過程中，當注水時間為t時，我們把容器甲的水位高度記為h_甲，容器乙的水位高度記為h_乙，設h_乙-h_甲=h,已知h（米）關于注水時間t（小時）的函數圖象如圖③所示，其中MN平行于橫軸，根據圖中所給信息，解決下列問題：
  ①求a的值；
  ②求圖③中線段PN所在直線的解析式．
  
  組卷：2143引用：4難度：0.1

  解析

• 28．如圖，在平面直角坐標系中，一次函數y=-

  2

  3

  x+4的圖象與x軸和y軸分別相交于A、B兩點．動點P從點A出發，在線段AO上以每秒3個單位長度的速度向點O做勻速運動，到達點O停止運動，點A關于點P的對稱點為點Q，以線段PQ為邊向上作正方形PQMN．設運動時間為t秒．
  （1）當t=

  1

  3

  秒時，點Q的坐標是

  ；
  （2）在運動過程中，設正方形PQMN與△AOB重疊部分的面積為S，求S與t的函數表達式；
  （3）若正方形PQMN對角線的交點為T，請直接寫出在運動過程中OT+PT的最小值．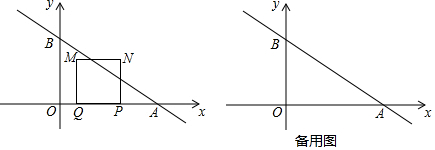
  
  組卷：4174引用：6難度：0.1

  解析