當前位置：試卷中心 > 試卷詳情

2021-2022學年山西省太原市小店區新時代雙語學校九年級（上）月考數學試卷（12月份）

發布：2024/8/27 9:0:9

一、選擇題（每小題3分，共30分）

1．如果
a
b
=
2
3
，則
a
+
b
b
等于（　　）
A．1
1
3
B．
1
2
C．
3
5
D．
5
3
組卷：238引用：18難度：0.9
解析
2．用配方法解一元二次方程x²-8x+5=0，將其化成（x+a）²=b的形式，則變形正確的是（　　）
A．（x+4）²=11 B．（x-4）²=21 C．（x-8）²=11 D．（x-4）²=11
組卷：2505引用：38難度：0.7
解析
3．菱形、矩形、正方形都具有的性質是（　　）
A．對角線相等 B．對角線互相垂直
C．對角線互相平分 D．對角線平分一組對角
組卷：450引用：31難度：0.9
解析
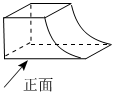4．畫如圖所示物體的俯視圖，正確的是（　　）
A． B． C． D．
組卷：876引用：12難度：0.9
解析
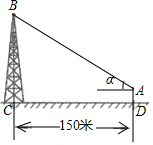5．如圖，在離鐵塔150米的A處，用測傾儀測得塔頂的仰角為α，測傾儀高AD為1.5米，則鐵塔的高BC為（　　）
A．（1.5+150tanα）米 B．（1.5+
150
tanα
）米
C．（1.5+150sinα）米 D．（1.5+
150
sinα
）米
組卷：3010引用：22難度：0.5
解析
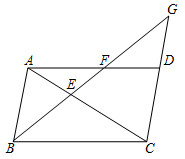6．如圖，在平行四邊形ABCD中，∠ABC的平分線交AC于點E，交AD于點F，交CD的延長線于點G，若AF=2FD，則
BE
EG
的值為（　　）
A．
1
2
B．
1
3
C．
2
3
D．
3
4
組卷：6723引用：38難度：0.5
解析
7．函數
y
=
k
x
和y=-kx+2（k≠0）在同一平面直角坐標系中的大致圖象可能是（　　）
A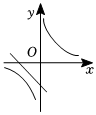． B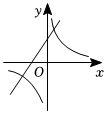． C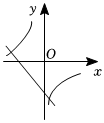． D．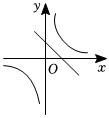
組卷：2529引用：29難度：0.6
解析

當前模式為游客模式，立即登錄查看試卷全部內容及下載

三、解答題（共8小題，滿分51分）

22．綜合與實踐：矩形的旋轉
問題情境：
在綜合與實踐課上，老師讓同學們以“矩形的旋轉”為主題開展數學活動．具體要求：如圖1，將長與寬都相等的兩個矩形紙片ABCD和EFGH疊放在一起，這時對角線AC和EG互相重合．固定矩形ABCD，將矩形EFGH繞AC的中點O逆時針方向旋轉，直到點E與點B重合時停止，在此過程中開展探究活動．
操作發現：
（1）雄鷹小組初步發現：在旋轉過程中，當邊AB與EF交于點M，邊CD與GH交于點N，如圖2、圖3所示，則線段AM與CN始終存在的數量關系是
．
（2）雄鷹小組繼續探究發現：在旋轉開始后，當兩個矩形紙片重疊部分為四邊形QMRN時，如圖3所示，四邊形QMRN為菱形，請你證明這個結論．
（3）雄鷹小組還發現在問題（2）中的四邊形QMRN中∠MQN與旋轉角∠AOE存在著特定的數量關系，請你寫出這一關系，并說明理由．
實踐探究：
（4）在圖3中，隨著矩形紙片EFGH的旋轉，四邊形QMRN的面積會發生變化．若矩形紙片的長為
2
+
2
，寬為
2
，請你幫助雄鷹小組探究當旋轉角∠AOE為多少度時，四邊形QMRN的面積最大？最大面積是多少？（直接寫出答案）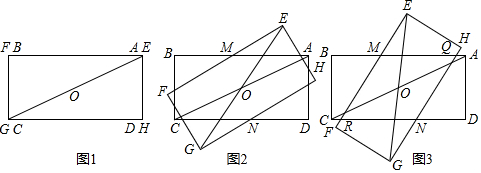
組卷：282引用：2難度：0.1
解析
23．已知，矩形OCBA在平面直角坐標系中的位置如圖所示，點C在x軸的正半軸上，點A在y軸的正半軸上，已知點B的坐標為（4，2），反比例函數y=
k
x
的圖象經過AB的中點D，且與BC交于點E，設直線DE的解析式為y=mx+n,連接OD，OE．
（1）求反比例函數y=
k
x
的表達式和點E的坐標；
（2）直接寫出不等式
k
x
＞mx+n的解集；
（3）點M為y軸正半軸上一點，若△MBO的面積等于△ODE的面積，求點M的坐標；
（4）點P為x軸上一點，點Q為反比例函數y=
k
x
圖象上一點，是否存在點P、Q使得以點P，Q，D，E為頂點的四邊形為平行四邊形？若存在，直接寫出點Q的坐標；若不存在，請說明理由．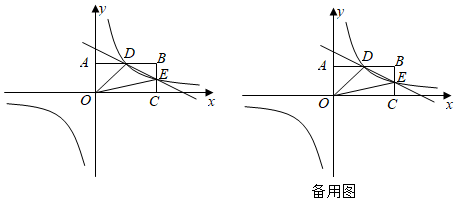
組卷：1209引用：3難度：0.4
解析