人教新版九年級上冊《22.2 二次函數(shù)與一元二次方程》2021年同步練習卷（3）

一、選擇題（本題共計7小題，每題3分，共計21分，）

• 1．二次函數(shù)y=kx²-6x+3的圖象與x軸有交點，則k的取值范圍是（　　）

  A．k＜3

  B．k＜3且k≠0

  C．k≤3

  D．k≤3且k≠0
  組卷：8086引用：138難度：0.9

  解析

• 2．拋物線y=-3x²+2x-1與坐標軸的交點個數(shù)為（　　）

  A．0個

  B．1個

  C．2個

  D．3個
  組卷：504引用：10難度：0.9

  解析

• 3．根據(jù)關于x的一元二次方程x²+px+q=0，可列表如下：
  

  x	0	0.5	1	1.1	1.2	1.3
  x2+px+q	-15	-8.75	-2	-0.59	0.84	2.29

  則方程x²+px+q=0的一個根滿足（　　）

  A．整數(shù)部分是0，十分位是5

  B．整數(shù)部分是0，十分位是8

  C．整數(shù)部分是1，十分位是1

  D．整數(shù)部分是1，十分位是2
  組卷：232引用：2難度：0.7

  解析

• 4．若二次函數(shù)y=ax²+bx+c（a≠0）的圖象與x軸有兩個交點，坐標分別為（x₁，0）、（x₂，0），且x₁＜x₂，圖象上有一點M（x₀，y₀），在x軸下方，則下列判斷正確的是（　　）

  A．a（x0-x1）（x0-x2）＜0	B．a＞0
  C．b2-4ac≥0	D．x1＜x0＜x2
  組卷：2992引用：57難度：0.7

  解析

• 5．已知二次函數(shù)y=ax²+bx+c的y與x的部分對應值如下表：則下列判斷中正確的是（　　）

  x	…	-1	0	1	2	…
  y	…	-5	1	3	1	…

  A．拋物線開口向上

  B．拋物線與y軸交于負半軸

  C．當x=3時，y＜0

  D．方程ax2+bx+c=0有兩個相等實數(shù)根
  組卷：717引用：12難度：0.9

  解析

• 6．拋物線y=ax²+2ax+a²+2的一部分如圖所示，那么該拋物線在y軸右側與x軸交點的坐標是（　　）

  A．（ 1 2 ，0）

  B．（1，0）

  C．（2，0）

  D．（3，0）
  組卷：517引用：25難度：0.9

  解析

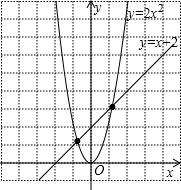• 7．探究課上，老師給出一個問題“利用二次函數(shù)y=2x²與一次函數(shù)y=x+2的圖象，求一元二次方程2x²=x+2的近似根”小華利用計算機繪制出如圖所示的圖象，通過觀察可知該方程的兩近似根x₁和x₂滿足-1＜x₁＜0，1＜x₂＜2．小華的上述方法體現(xiàn)的數(shù)學思想是（　　）

  A．公理化	B．分類討論
  C．數(shù)形結合	D．由特殊到一般
  組卷：557引用：6難度：0.6

  解析

三、解答題（本題共計8小題，共計75分，）

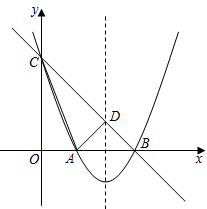• 22．如圖，頂點坐標為（2，-1）的拋物線y=ax²+bx+c（a≠0）與y軸交于點C（0，3），與x軸交于A，B兩點．
  （1）求拋物線的表達式；
  （2）設拋物線的對稱軸與直線BC交于點D，連接AC，AD，求△ACD的面積．
  組卷：27引用：1難度：0.5

  解析

• 23．關于x的一元二次方程（m²-1）x²-2（m-2）x+1=0．
  （1）當m為何值時，方程有兩個不相等的實數(shù)根；
  （2）點A（-1，-1）是拋物線y=（m²-1）x²-2（m-2）x+1上的點，求拋物線的解析式；
  （3）在（2）的條件下，若點B與點A關于拋物線的對稱軸對稱，是否存在與拋物線只交于點B的直線，若存在，請求出直線的解析式；若不存在，請說明理由．
  組卷：108引用：2難度：0.3

  解析