2018-2019學(xué)年重慶八中九年級(jí)（上）開學(xué)數(shù)學(xué)試卷

一、選擇題：（本大題12個(gè)小題，每小題4分，共48分）在每個(gè)小題的下面，都給出了代號(hào)為A、B、c、D的四個(gè)答案，其中只有一個(gè)是正確的，請(qǐng)將答題卡上題號(hào)右側(cè)正確答案所對(duì)應(yīng)的方框涂黑

• 1．-2的倒數(shù)是（　　）

  A．-2

  B．- 1 2

  C． 1 2

  D．2
  組卷：4010引用：688難度：0.9

  解析

• 2．下列全國(guó)各地地鐵標(biāo)志圖中，既是軸對(duì)稱圖形又是中心對(duì)稱圖形的是（　　）

  A．

  B．

  C．

  D．
  組卷：1038引用：38難度：0.9

  解析

• 3．計(jì)算（-2x³y）²的結(jié)果是（　　）

  A．4x5y2

  B．-4x5y2

  C．4x6y2

  D．-4x6y2
  組卷：305引用：7難度：0.9

  解析

• 4．估計(jì)（2

  30

  -

  24

  ）?

  1

  6

  的值應(yīng)在（　　）

  A．1和2之間

  B．2和3之間

  C．3和4之間

  D．4和5之間
  組卷：1893引用：20難度：0.9

  解析

• 5．下列命題正確的是（　　）

  A．平行四邊形的對(duì)角線互相垂直平分

  B．矩形的對(duì)角線互相垂直平分

  C．菱形的對(duì)角線互相平分且相等

  D．正方形的對(duì)角線互相垂直平分
  組卷：862引用：16難度：0.7

  解析

• 6．已知x-y=3，xy=1，則代數(shù)式3xy-5x+5y的值為（　　）

  A．-12

  B．-14

  C．12

  D．14
  組卷：237引用：2難度：0.8

  解析

• 7．關(guān)于x的一元二次方程kx²-6x+9=0有兩個(gè)不相等的實(shí)數(shù)根，那么k的取值范圍是（　　）

  A．k＜1

  B．k≠0

  C．k＜1且k≠0

  D．k＞1
  組卷：694引用：43難度：0.9

  解析

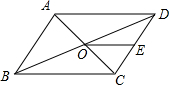• 8．如圖，平行四邊形ABCD中，對(duì)角線AC，BD相交于點(diǎn)O，點(diǎn)E是CD的中點(diǎn)，則△ODE與△AOB的面積比為（　　）

  A．1：2

  B．1：3

  C．1：4

  D．1：5
  組卷：1692引用：10難度：0.8

  解析

四、解答題：（本大題5個(gè)小題，每小題10分，共50分）解答時(shí)每小題必須給出必要的演算過程或推理步驟，請(qǐng)將解答書寫在答題卡（卷）中對(duì)應(yīng)的位置上

• 25．在一個(gè)m（m≥3，m為整數(shù)）位的正整數(shù)中，若從左到右第n（n≤m,n為正整數(shù)）位上的數(shù)字與從右到左第n位上的數(shù)字之和都等于同一個(gè)常數(shù)k（k為正整數(shù)），則稱這樣的數(shù)為“平衡數(shù)”．例如在正整數(shù)3186中，因?yàn)?+6=1+8-9，所以3186是“平衡數(shù)”，其中k=9，再如在正整數(shù)53697中，因?yàn)?+7=3+9=6+6=12，所以53697是“平衡數(shù)”，其中k=12．
  （1）已知在一個(gè)能被11整除的四位“平衡數(shù)”中k=4，設(shè)這個(gè)四位“平衡數(shù)”的千位上的數(shù)字為s（1≤s≤9，s為整數(shù)），百位上的數(shù)字為t（0≤t≤9，t為整數(shù)），

  st

  2

  是整數(shù)，求這個(gè)四位“平衡數(shù)“．
  （2）在一個(gè)四位正整數(shù)A=

  m

  88

  n

  （1≤m≤9，0≤n≤9，m,m為整數(shù)）中，m+n=11，數(shù)

  A

  9

  恰等于一個(gè)三位“平衡數(shù)”，設(shè)這個(gè)三位“平衡數(shù)”百位上的數(shù)字為x（1≤x≤9，x為整數(shù)），十位上的數(shù)字為y,求證：y=x-1．
  組卷：282引用：1難度：0.5

  解析

五、解答題：（本大題1個(gè)小題，12分）解答時(shí)每小題必須給出必要的演算過程或推理步驟，請(qǐng)將解答書寫在答題卡卷）中對(duì)應(yīng)的位置上

• 26．如圖，平面直角坐標(biāo)系中，直線AB與x軸、y軸分別交于點(diǎn)A、B，直線CD與x軸、y軸分別交于點(diǎn)C、D，AB與CD相交于點(diǎn)E，線段OA、OC的長(zhǎng)是一元二次方程x²-18x+72=0的兩根（OA＞OC），OB=

  4

  3

  OA，點(diǎn)E的橫坐標(biāo)為3，反比例函數(shù)y=

  k

  x

  的圖象經(jīng)過點(diǎn)E．
  （1）求k的值；
  （2）若直線AB與反比例函數(shù)圖象上除點(diǎn)E外的另一交點(diǎn)為P，求△ECP的面積；若點(diǎn)R在x軸上，若點(diǎn)S在y軸上，求PR+RS+SE的最小值；
  （3）若點(diǎn)M在坐標(biāo)軸上，在平面內(nèi)是否存在一點(diǎn)N，使以點(diǎn)C、E、M、N為頂點(diǎn)的四邊形是矩形且線段CE為矩形的一條邊？若存在，直接寫出符合條件的N點(diǎn)坐標(biāo)；若不存在，請(qǐng)說(shuō)明理由．
  
  組卷：1160引用：2難度：0.3

  解析