人教五四新版九年級（上）中考題單元試卷：第28章 二次函數（27）

一、選擇題（共1小題）

• 1．如圖，在10×10的網格中，每個小方格都是邊長為1的小正方形，每個小正方形的頂點稱為格點．若拋物線經過圖中的三個格點，則以這三個格點為頂點的三角形稱為拋物線的“內接格點三角形”．以O為坐標原點建立如圖所示的平面直角坐標系，若拋物線與網格對角線OB的兩個交點之間的距離為

  3

  2

  ，且這兩個交點與拋物線的頂點是拋物線的內接格點三角形的三個頂點，則滿足上述條件且對稱軸平行于y軸的拋物線條數是（　　）

  A．16

  B．15

  C．24

  D．13
  組卷：132引用：60難度：0.4

  解析

二、填空題（共2小題）

• 2．在平面直角坐標系xOy中，直線y=kx（k為常數）與拋物線y=

  1

  3

  x²-2交于A，B兩點，且A點在y軸左側，P點的坐標為（0，-4），連接PA，PB．有以下說法：
  ①PO²=PA?PB；
  ②當k＞0時，（PA+AO）（PB-BO）的值隨k的增大而增大；
  ③當k=

  -

  3

  3

  時，BP²=BO?BA；
  ④△PAB面積的最小值為

  4

  6

  ．
  其中正確的是

  ．（寫出所有正確說法的序號）
  組卷：3846引用：57難度：0.1

  解析

• 3．二次函數y=

  2

  3

  x

  2

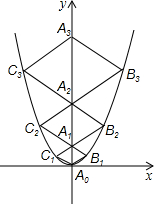  的圖象如圖，點A₀位于坐標原點，點A₁，A₂，A₃…A_n在y軸的正半軸上，點B₁，B₂，B₃…B_n在二次函數位于第一象限的圖象上，點C₁，C₂，C₃…C_n在二次函數位于第二象限的圖象上，四邊形A₀B₁A₁C₁，四邊形A₁B₂A₂C₂，四邊形A₂B₃A₃C₃…四邊形A_n-1B_nA_nC_n都是菱形，∠A₀B₁A₁=∠A₁B₂A₂=∠A₂B₃A₃…=∠A_n-1B_nA_n=60°，菱形A_n-1B_nA_nC_n的周長為

  ．
  組卷：2791引用：68難度：0.7

  解析

三、解答題（共27小題）

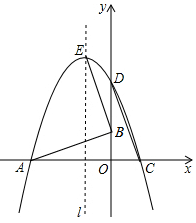• 4．如圖，已知△OAB的頂點A（-6，0），B（0，2），O是坐標原點，將△OAB繞點O按順時針旋轉90°，得到△ODC．
  （1）寫出C，D兩點的坐標；
  （2）求過A，D，C三點的拋物線的解析式，并求此拋物線頂點E的坐標；
  （3）證明AB⊥BE．
  組卷：511引用：56難度：0.5

  解析

• 5．如圖，頂點為A的拋物線y=a（x+2）²-4交x軸于點B（1，0），連接AB，過原點O作射線OM∥AB，過點A作AD∥x軸交OM于點D，點C為拋物線與x軸的另一個交點，連接CD．
  （1）求拋物線的解析式（關系式）；
  （2）求點A，B所在的直線的解析式（關系式）；
  （3）若動點P從點O出發，以每秒1個單位長度的速度沿著射線OM運動，設點P運動的時間為t秒，問：當t為何值時，四邊形ABOP分別為平行四邊形？等腰梯形？
  （4）若動點P從點O出發，以每秒1個單位長度的速度沿線段OD向點D運動，同時動點Q從點C出發，以每秒2個單位長度的速度沿線段CO向點O運動，當其中一個點停止運動時另一個點也隨之停止運動．設它們的運動時間為t秒，連接PQ．問：當t為何值時，四邊形CDPQ的面積最小？并求此時PQ的長．
  組卷：381引用：53難度：0.5

  解析

• 6．已知：拋物線C₁：y=x²．如圖（1），平移拋物線C₁得到拋物線C₂，C₂經過C₁的頂點O和A（2，0），C₂的對稱軸分別交C₁、C₂于點B、D．
  （1）求拋物線C₂的解析式；
  （2）探究四邊形ODAB的形狀并證明你的結論；
  （3）如圖（2），將拋物線C₂向m個單位下平移（m＞0）得拋物線C₃，C₃的頂點為G，與y軸交于M．點N是M關于x軸的對稱點，點P（-

  4

  3

  m,

  1

  3

  m）在直線MG上．問：當m為何值時，在拋物線C₃上存在點Q，使得以M、N、P、Q為頂點的四邊形為平行四邊形？
  
  組卷：431引用：54難度：0.5

  解析

• 7．拋物線y=-x²平移后的位置如圖所示，點A，B坐標分別為（-1，0）、（3，0），設平移后的拋物線與y軸交于點C，其頂點為D．
  （1）求平移后的拋物線的解析式和點D的坐標；
  （2）∠ACB和∠ABD是否相等？請證明你的結論；
  （3）點P在平移后的拋物線的對稱軸上，且△CDP與△ABC相似，求點P的坐標．
  組卷：434引用：51難度：0.5

  解析

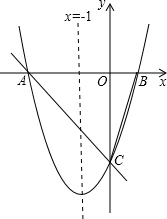• 8．如圖，對稱軸為直線x=-1的拋物線y=ax²+bx+c（a≠0）與x軸相交于A、B兩點，其中點A的坐標為（-3，0）．
  （1）求點B的坐標．
  （2）已知a=1，C為拋物線與y軸的交點．
  ①若點P在拋物線上，且S_△POC=4S_△BOC，求點P的坐標．
  ②設點Q是線段AC上的動點，作QD⊥x軸交拋物線于點D，求線段QD長度的最大值．
  組卷：3980引用：91難度：0.3

  解析

• 9．如圖，已知拋物線y=x²+bx+c與x軸交于點A，B，AB=2，與y軸交于點C，對稱軸為直線x=2．
  （1）求拋物線的函數表達式；
  （2）設P為對稱軸上一動點，求△APC周長的最小值；
  （3）設D為拋物線上一點，E為對稱軸上一點，若以點A，B，D，E為頂點的四邊形是菱形，則點D的坐標為

  ．
  組卷：693引用：59難度：0.1

  解析

• 10．如圖1，拋物線y=-

  2

  3

  x²+bx+c與x軸相交于點A，C，與y軸相交于點B，連接AB，BC，點A的坐標為（2，0），tan∠BAO=2，以線段BC為直徑作⊙M交AB于點D，過點B作直線l∥AC，與拋物線和⊙M的另一個交點分別是E，F．
  （1）求該拋物線的函數表達式；
  （2）求點C的坐標和線段EF的長；
  （3）如圖2，連接CD并延長，交直線l于點N，點P，Q為射線NB上的兩個動點（點P在點Q的右側，且不與N重合），線段PQ與EF的長度相等，連接DP，CQ，四邊形CDPQ的周長是否有最小值？若有，請求出此時點P的坐標并直接寫出四邊形CDPQ周長的最小值；若沒有，請說明理由．
  
  組卷：1273引用：51難度：0.5

  解析

三、解答題（共27小題）

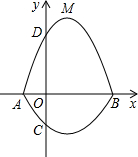• 29．如圖，在平面直角坐標系xOy中，A、B為x軸上兩點，C、D為y軸上的兩點，經過點A、C、B的拋物線的一部分C₁與經過點A、D、B的拋物線的一部分C₂組合成一條封閉曲線，我們把這條封閉曲線稱為“蛋線”．已知點C的坐標為（0，-

  3

  2

  ），點M是拋物線C₂：y=mx²-2mx-3m（m＜0）的頂點．
  （1）求A、B兩點的坐標；
  （2）“蛋線”在第四象限上是否存在一點P，使得△PBC的面積最大？若存在，求出△PBC面積的最大值；若不存在，請說明理由；
  （3）當△BDM為直角三角形時，求m的值．
  組卷：2305引用：83難度：0.5

  解析

• 30．如圖1，已知拋物線y=ax²+bx（a≠0）經過A（3，0）、B（4，4）兩點．
  （1）求拋物線的解析式；
  （2）將直線OB向下平移m個單位長度后，得到的直線與拋物線只有一個公共點D，求m的值及點D的坐標；
  （3）如圖2，若點P為平面上一點，點N在拋物線上，且∠NBO=∠ABO，則在（2）的條件下，求出所有滿足△POD∽△NOB的點P坐標（點P、O、D分別與點N、O、B對應）．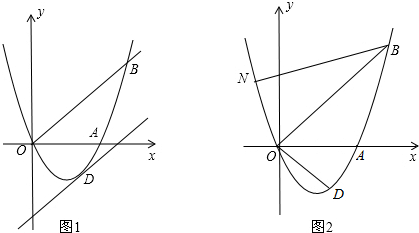
  
  組卷：2140引用：68難度：0.5

  解析