2022-2023學(xué)年浙江省寧波市鄞州區(qū)部分學(xué)校九年級（上）期末數(shù)學(xué)試卷

一、選擇題（每題4分，共40分）

• 1．計算

  8

  +|-2|×cos45°的結(jié)果，正確的是（　　）

  A． 2

  B．3 2

  C．2 2 + 3

  D．2 2 +2
  組卷：379引用：6難度：0.8

  解析

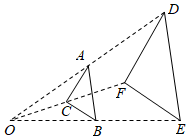• 2．如圖，△ABC與△DEF位似，點(diǎn)O是它們的位似中心，其中OE=2OB，則△ABC與△DEF的周長之比是（　　）

  A．1：2

  B．1：4

  C．1：3

  D．1：9
  組卷：2756引用：44難度：0.7

  解析

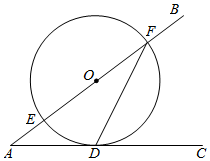• 3．如圖，∠BAC=36°，點(diǎn)O在邊AB上，⊙O與邊AC相切于點(diǎn)D，交邊AB于點(diǎn)E，F(xiàn)，連接FD，則∠AFD等于（　　）

  A．27°

  B．29°

  C．35°

  D．37°
  組卷：3295引用：34難度：0.6

  解析

• 4．某學(xué)校組織學(xué)生到社區(qū)開展公益宣傳活動，成立了“垃圾分類”“文明出行”“低碳環(huán)保”三個宣傳隊，如果小華和小麗每人隨機(jī)選擇參加其中一個宣傳隊，則她們恰好選到同一個宣傳隊的概率是（　　）

  A． 1 9

  B． 1 6

  C． 1 3

  D． 2 3
  組卷：2557引用：35難度：0.5

  解析

• 5．如圖，AC為矩形ABCD的對角線，已知AD=3，CD=4，點(diǎn)P沿折線C-A-D以每秒1個單位長度的速度運(yùn)動（運(yùn)動到D點(diǎn)停止），過點(diǎn)P作PE⊥BC于點(diǎn)E，則△CPE的面積y與點(diǎn)P運(yùn)動的路程x間的函數(shù)圖象大致是（　　）

  A．

  B．

  C．

  D．
  組卷：2684引用：32難度：0.5

  解析

• 6．在平面直角坐標(biāo)系中，已知二次函數(shù)y=ax²+bx+c（a≠0）的圖象如圖所示，有下列5個結(jié)論：
  ①abc＞0；②2a-b=0；③9a+3b+c＞0；④b²＞4ac；⑤a+c＜b.
  其中正確的有（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：3727引用：22難度：0.6

  解析

• 7．已知a,b是非零實數(shù)，且|a|＞|b|，在同一個坐標(biāo)系中，二次函數(shù)y=ax²+bx與一次函數(shù)y=ax+b的圖象可能是（　　）

  A．

  B．

  C．

  D．
  組卷：917引用：7難度：0.5

  解析

• 8．在平面直角坐標(biāo)系中，已知點(diǎn)（1，m），（3，n）在拋物線y=ax²+bx上，且mn＜0．設(shè)

  t

  =

  -

  b

  2

  a

  ，則t的值可以是（　　）

  A． 1 3

  B． 1 2

  C．1

  D． 3 2
  組卷：972引用：6難度：0.4

  解析

三、解答題（共80分）

• 23．定義：若一個四邊形能被其中的一條對角線分割成兩個相似三角形，則稱這個四邊形為“師梅四邊形”，這條對角線稱為“師梅線”．我們熟知的平行四邊形就是“師梅四邊形”．
  
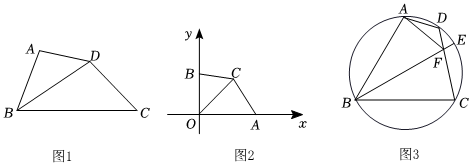
  （1）如圖1，BD平分∠ABC，

  BD

  =

  4

  2

  ，BC=10．四邊形ABCD是被BD分割成的“師梅四邊形”，求AB長；
  （2）如圖2，平面直角坐標(biāo)系中，A、B分別是x軸和y軸上的點(diǎn)，且OA=3，OB=2，若點(diǎn)C是直線y=x在第一象限上的一點(diǎn)，且OC是四邊形OACB的“師梅線”，求四邊形OACB的面積；
  （3）如圖3，圓內(nèi)接四邊形ABCD中，∠ABC=60°，點(diǎn)E是

  ?

  AC

  的中點(diǎn)，連接BE交CD于點(diǎn)F，連接AF，∠DAF=30°，
  ①求證：四邊形ABCF是“師梅四邊形”；
  ②若△ABC的面積為

  6

  3

  ，求線段BF的長．
  組卷：1172引用：9難度：0.1

  解析

• 24．綜合與實踐
  “善思”小組開展“探究四點(diǎn)共圓的條件”活動，得出結(jié)論：對角互補(bǔ)的四邊形四個頂點(diǎn)共圓．該小組繼續(xù)利用上述結(jié)論進(jìn)行探究．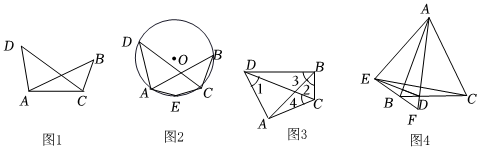
  
  提出問題：
  如圖1，在線段AC同側(cè)有兩點(diǎn)B，D，連接AD，AB，BC，CD，如果∠ABC=∠ADC，那么A，B，C，D四點(diǎn)在同一個圓上．
  探究展示：求證：點(diǎn)A，B，C，D四點(diǎn)在同一個圓上．
  如圖2，作經(jīng)過點(diǎn)A，C，D的⊙O，在劣弧AC上取一點(diǎn)E（不與A，C重合），連接AE，CE，則∠AEC+∠D=180°
  

  ．
  （1）請完善探究展示．
  （2）如圖3，在四邊形ABCD中，∠1=∠2，∠3=45°，則∠4的度數(shù)為

  ．
  拓展探究：
  （3）如圖4，已知△ABC是等腰三角形，AB=AC，點(diǎn)D在BC上（不與BC的中點(diǎn)重合），連接AD．作點(diǎn)C關(guān)于AD的對稱點(diǎn)E，連接EB并延長交AD的延長線于F，連接AB，DE．
  ①求證：A，D，B，E四點(diǎn)共圓；
  ②若AB=2

  2

  ，AD?AF的值是否會發(fā)生變化，若不變化，求出其值；若變化，請說明理由．
  組卷：761引用：2難度：0.3

  解析