2022-2023學(xué)年上海市黃浦區(qū)八年級（下）期中數(shù)學(xué)試卷

一、選擇題（本大題共6題，每題3分，總分18分）

• 1．下列說法正確的是（　　）

  A． x 2 + y = 2 是二元二次方程	B．x2-x=0是二項方程
  C． x 2 - x 3 = 2 是分式方程	D． x 2 - x x = 2 是無理方程
  組卷：232引用：6難度：0.9

  解析

• 2．一次函數(shù)y=-2（x-3）在y軸上的截距是（　　）

  A．2

  B．-3

  C．-6

  D．6
  組卷：196引用：1難度：0.6

  解析

• 3．直線y=（

  1

  2

  k-1）x+2（1-k）的圖象經(jīng)過第一、二、四象限，那么k的取值范圍是（　　）

  A．k＞2

  B．k＜2

  C．k＞1

  D．k＜1
  組卷：928引用：2難度：0.5

  解析

• 4．如果關(guān)于x的方程（m+2）x=8無解，那么m的取值范圍是（　　）

  A．m＞-2

  B．m=-2

  C．m≠-2

  D．任意實數(shù)
  組卷：253引用：1難度：0.9

  解析

• 5．在下列方程中，有實數(shù)根的方程的個數(shù)有（　　）
  ①

  x

  +

  2

  +

  3

  =

  0

  ；
  ②

  x

  -

  4

  +

  3

  -

  x

  =

  0

  ；
  ③

  x

  +

  1

  =

  -

  x

  ；
  ④

  2

  x

  -

  3

  +

  3

  -

  2

  x

  =

  0

  ；
  ⑤x²-2x+4=0；
  ⑥

  2

  x

  +

  1

  +

  3

  x

  -

  1

  =

  6

  x

  2

  -

  1

  ．

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：110引用：1難度：0.6

  解析

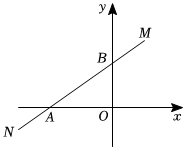• 6．如圖，已知直線MN：y=

  3

  3

  x+2交x軸負(fù)半軸于點A，交y軸于點B，點C是x軸上的一點，且OC=2，則∠MBC的度數(shù)為（　　）

  A．45°或135°

  B．30°或150°

  C．60°或120°

  D．75°或165°
  組卷：829引用：3難度：0.4

  解析

二、填空題（本大題共12題，每題2分，總分24分）

• 7．已知函數(shù)f（x）=

  2

  x+1，那么f（

  2

  ）=

  ．
  組卷：93引用：3難度：0.9

  解析

• 8．若y=（m-2）x+m²-5m+5是y關(guān)于x的正比例函數(shù)，則m=

  ．
  組卷：310引用：1難度：0.8

  解析

四、解答題（本大題共2題，每題9分，總分18分）

• 25．“程，課程也，二物者二程，三物者三程，皆如物數(shù)程之，并列為行，故謂之方程．”這是我國古代著名數(shù)學(xué)家劉徽在《九章算術(shù)》對方程一詞給出的注釋，對于一些特殊的方程，我們給出兩個定義：①若兩個方程有相同的一個解，則稱這兩個方程為“相似方程”；②若兩個方程有相同的整數(shù)解，則稱這兩個方程為“相伴方程”．
  （1）判斷分式方程

  1

  1

  -

  x

  +

  1

  =

  2

  1

  +

  x

  與無理方程

  x

  2

  -

  2

  =

  2

  x

  +

  1

  是否是“相似方程”，并說明理由；
  （2）已知關(guān)于x,y的方程：4x²+9y²=8-12xy和2x+3y=4，它們是“相似方程”嗎？如果是，請寫出它們的公共解；如果不是，請說明理由；
  （3）已知關(guān)于x,y的二元一次方程：y=（k+1）x-4和x=y+3k（其中k為整數(shù)）是“相伴方程”，求k的值．
  組卷：360引用：1難度：0.3

  解析

五、綜合題（本大題10分）

• 26．已知：點P（1，m）、

  Q

  （

  n

  ,

  1

  2

  ）

  在反比例函數(shù)y=

  3

  2

  x

  的圖象上，直線y=kx+b經(jīng)過點P、Q，且與x軸，y軸的交點分別為A、B兩點．
  （1）求直線AB的表達(dá)式；
  （2）O為坐標(biāo)原點，C在直線PQ上且滿足AB=AC，點D在坐標(biāo)平面內(nèi)，順次聯(lián)結(jié)點O、B、C、D的四邊形滿足：BC∥OD，BO=CD，求D點坐標(biāo)．
  組卷：172引用：1難度：0.5

  解析