冀教新版八年級（上）中考題單元試卷：第17章 特殊三角形（04）

一、選擇題（共13小題）

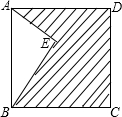• 1．如圖，點E在正方形ABCD內(nèi)，滿足∠AEB=90°，AE=6，BE=8，則陰影部分的面積是（　　）

  A．48

  B．60

  C．76

  D．80
  組卷：3536引用：139難度：0.9

  解析

• 2．如圖，△ABC中，D為AB中點，E在AC上，且BE⊥AC．若DE=10，AE=16，則BE的長度為何？（　　）

  A．10

  B．11

  C．12

  D．13
  組卷：1259引用：76難度：0.9

  解析

• 3．如圖，在邊長為1個單位長度的小正方形組成的網(wǎng)格中，點A、B都是格點，則線段AB的長度為（　　）

  A．5

  B．6

  C．7

  D．25
  組卷：4164引用：89難度：0.9

  解析

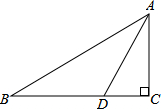• 4．如圖，在△ABC中，∠C=90°，AC=2，點D在BC上，∠ADC=2∠B，AD=

  5

  ，則BC的長為（　　）

  A． 3 -1

  B． 3 +1

  C． 5 -1

  D． 5 +1
  組卷：18671引用：61難度：0.9

  解析

• 5．如圖，矩形紙片ABCD中，點E是AD的中點，且AE=1，BE的垂直平分線MN恰好過點C．則矩形的一邊AB的長度為（　　）

  A．1

  B． 2

  C． 3

  D．2
  組卷：3397引用：75難度：0.7

  解析

• 6．如圖，在Rt△ABC中，∠BAC=90°，∠ABC的平分線BD交AC于點D，DE是BC的垂直平分線，點E是垂足．已知DC=8，AD=4，則圖中長為4

  3

  的線段有（　　）

  A．4條

  B．3條

  C．2條

  D．1條
  組卷：2786引用：51難度：0.7

  解析

• 7．△ABC中，AB=AC=5，BC=8，點P是BC邊上的動點，過點P作PD⊥AB于點D，PE⊥AC于點E，則PD+PE的長是（　　）

  A．4.8

  B．4.8或3.8

  C．3.8

  D．5
  組卷：17164引用：59難度：0.5

  解析

• 8．如圖，在四邊形ABCD中，AD∥BC，DE⊥BC，垂足為點E，連接AC交DE于點F，點G為AF的中點，∠ACD=2∠ACB．若DG=3，EC=1，則DE的長為（　　）

  A．2 3

  B． 10

  C．2 2

  D． 6
  組卷：5882引用：76難度：0.5

  解析

• 9．在邊長為正整數(shù)的△ABC中，AB=AC，且AB邊上的中線CD將△ABC的周長分為1：2的兩部分，則△ABC面積的最小值為（　　）

  A． 7 12

  B． 7 36 15

  C． 3 4 7

  D． 7 4 15
  組卷：2507引用：50難度：0.5

  解析

• 10．如圖，△ABC中，BC=AC，D、E兩點分別在BC與AC上，AD⊥BC，BE⊥AC，AD與BE相交于F點．若AD=4，CD=3，則關(guān)于∠FBD、∠FCD、∠FCE的大小關(guān)系，下列何者正確？（　　）

  A．∠FBD＞∠FCD

  B．∠FBD＜∠FCD

  C．∠FCE＞∠FCD

  D．∠FCE＜∠FCD
  組卷：850引用：51難度：0.5

  解析

三、解答題（共4小題）

• 29．如圖，根據(jù)圖中數(shù)據(jù)完成填空，再按要求答題：
  
  sin²A₁+sin²B₁=

  ；sin²A₂+sin²B₂=

  ；sin²A₃+sin²B₃=

  ．
  （1）觀察上述等式，猜想：在Rt△ABC中，∠C=90°，都有sin²A+sin²B=

  ．
  （2）如圖④，在Rt△ABC中，∠C=90°，∠A、∠B、∠C的對邊分別是a、b、c,利用三角函數(shù)的定義和勾股定理，證明你的猜想．
  （3）已知：∠A+∠B=90°，且sinA=

  5

  13

  ，求sinB．
  組卷：810引用：61難度：0.3

  解析

• 30．如圖，AB是⊙O的直徑，點C在⊙O上，連接BC，AC，作OD∥BC與過點A的切線交于點D，連接DC并延長交AB的延長線于點E．
  （1）求證：DE是⊙O的切線；
  （2）若

  CE

  DE

  =

  2

  3

  ，求cos∠ABC的值．
  組卷：1074引用：50難度：0.3

  解析