2022-2023學年北京師大三附中九年級（上）月考數學試卷（12月份）

一、選擇題（本題共16分，每小題2分）

• 1．下列圖形中，既是軸對稱圖形又是中心對稱圖形的是（　　）

  A．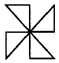

  B．

  C．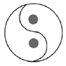

  D．
  組卷：154引用：11難度：0.9

  解析

• 2．拋物線y=3（x-1）²+2的頂點坐標為（　　）

  A．（-1，2）

  B．（1，-2）

  C．（1，2）

  D．（2，1）
  組卷：1594引用：16難度：0.8

  解析

• 3．將一元二次方程x²-8x+10=0通過配方轉化為（x+a）²=b的形式，下列結果中正確的是（　　）

  A．（x-4）2=6

  B．（x-8）2=6

  C．（x-4）2=-6

  D．（x-8）2=54
  組卷：1865引用：37難度：0.6

  解析

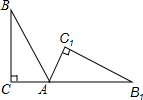• 4．如圖，將Rt△ABC（∠B=35°，∠C=90°）繞點A按順時針方向旋轉到△AB₁C₁的位置，使得點C，A，B₁在同一條直線上，那么旋轉角等于（　　）

  A．55°

  B．70°

  C．125°

  D．145°
  組卷：593引用：5難度：0.7

  解析

• 5．AB為⊙O的直徑，點C在⊙O上，若∠C=15°，則∠BOC=（　　）
  

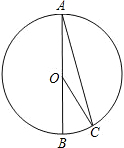
  A．60°

  B．45°

  C．30°

  D．15°
  組卷：43引用：9難度：0.9

  解析

• 6．已知點A（-3，y₁），B（2，y₂）均在拋物線y=-2（x-1）²+3上，則下列結論正確的是（　　）

  A．3＜y1＜y2

  B．3＜y2＜y1

  C．y2＜y1＜3

  D．y1＜y2＜3
  組卷：769引用：7難度：0.8

  解析

• 7．已知函數y=-x²+bx+c,其中b＞0，c＜0，此函數的圖象可以是（　　）

  A．

  B．

  C．

  D．
  組卷：403引用：8難度：0.7

  解析

• 8．做隨機拋擲一枚紀念幣的試驗，得到的結果如下表所示：
  

  拋擲次數m	500	1000	1500	2000	2500	3000	4000	5000
  “正面向上”的次數n	265	512	793	1034	1306	1558	2083	2598
  “正面向上”的頻率 n m	0.530	0.512	0.529	0.517	0.522	0.519	0.521	0.520

  下面有3個推斷：
  ①當拋擲次數是1000時，“正面向上”的頻率是0.512，所以“正面向上”的概率是0.512；
  ②隨著試驗次數的增加，“正面向上”的頻率總在0.520附近擺動，顯示出一定的穩定性，可以估計“正面向上”的概率是0.520；
  ③若再次做隨機拋擲該紀念幣的試驗，則當拋擲次數為3000時，出現“正面向上”的次數不一定是1558次．
  其中所有合理推斷的序號是（　　）

  A．②

  B．①③

  C．②③

  D．①②③
  組卷：919引用：11難度：0.7

  解析

二、填空題（本題共16分，每小題2分）

• 9．若關于x的一元二次方程x²+mx-2m=0的一根為1，則m的值是

  ．
  組卷：41引用：8難度：0.7

  解析

三、解答題（本題共68分，其中17-22每題5分，23-26題每題6分，27-28每題7分）

• 27．如圖，在正方形ABCD中，E是邊AB上的一動點（不與點A、B重合），連接DE，點A關于直線DE的對稱點為F，連接EF并延長交BC于點G，連接DG，過點E作EH⊥DE交DG的延長線于點H，連接BH．
  （1）求證：GF=GC；
  （2）用等式表示線段BH與AE的數量關系，并證明．
  組卷：12306引用：22難度：0.4

  解析

• 28．對于平面直角坐標系xOy中的圖形M，N，給出如下定義：P為圖形M上任意一點，Q為圖形N上任意一點，如果P，Q兩點間的距離有最小值，那么稱這個最小值為圖形M，N間的“閉距離“，記作d（M，N）．
  已知點A（-2，6），B（-2，-2），C（6，-2）．
  （1）求d（點O，△ABC）；
  （2）記函數y=kx（-1≤x≤1，k≠0）的圖象為圖形G．若d（G，△ABC）=1，直接寫出k的取值范圍；
  （3）⊙T的圓心為T（t,0），半徑為1．若d（⊙T，△ABC）=1，直接寫出t的取值范圍．
  組卷：4391引用：8難度：0.3

  解析