人教五四新版九年級（上）中考題單元試卷：第28章 二次函數（21）

一、選擇題（共1小題）

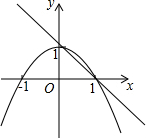• 1．如圖，已知拋物線y₁=-x²+1，直線y₂=-x+1，當x任取一值時，x對應的函數值分別為y₁，y₂．若y₁≠y₂，取y₁，y₂中的較小值記為M；若y₁=y₂，記M=y₁=y₂．例如：當x=2時，y₁=-3，y₂=-1，y₁＜y₂，此時M=-3．下列判斷中：
  ①當x＜0時，M=y₁；
  ②當x＞0時，M隨x的增大而增大；
  ③使得M大于1的x值不存在；
  ④使得M=

  1

  2

  的值是-

  2

  2

  或

  1

  2

  ，
  其中正確的個數有（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：2527引用：53難度：0.3

  解析

二、填空題（共1小題）

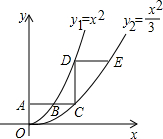• 2．如圖，平行于x軸的直線AC分別交函數y₁=x²（x≥0）與y₂=

  x

  2

  3

  （x≥0）的圖象于B、C兩點，過點C作y軸的平行線交y₁的圖象于點D，直線DE∥AC，交y₂的圖象于點E，則

  DE

  AB

  =

  ．
  組卷：6074引用：85難度：0.5

  解析

三、解答題（共28小題）

• 3．如圖（1），在平面直角坐標系xOy中，拋物線y=ax²+bx+c（a≠0）與x軸交于A（-1，0），B（3，0），與y軸交于C（0，3），頂點為D（1，4），對稱軸為DE．
  （1）拋物線的解析式是

   

  ；
  （2）如圖（2），點P是AD上一個動點，P′是P關于DE的對稱點，連接PE，過P′作P′F∥PE交x軸于F．設S_{四邊形EPP′F}=y,EF=x,求y關于x的函數關系式，并求y的最大值；
  （3）在（1）中的拋物線上是否存在點Q，使△BCQ成為以BC為直角邊的直角三角形？若存在，求出Q的坐標；若不存在．請說明理由．
  
  組卷：1159引用：52難度：0.5

  解析

• 4．如圖所示，拋物線y=ax²+bx+c的頂點為M（-2，-4），與x軸交于A、B兩點，且A（-6，0），與y軸交于點C．
  （1）求拋物線的函數解析式；
  （2）求△ABC的面積；
  （3）能否在拋物線第三象限的圖象上找到一點P，使△APC的面積最大？若能，請求出點P的坐標；若不能，請說明理由．
  組卷：37引用：69難度：0.5

  解析

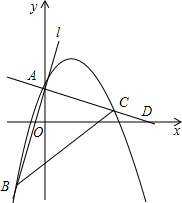• 5．如圖，拋物線y=ax²+bx+2與直線l交于點A、B兩點，且A點為拋物線與y軸的交點，B（-2，-4），拋物線的對稱軸是直線x=2，過點A作AC⊥AB，交拋物線于點C、x軸于點D．
  （1）求此拋物線的解析式；
  （2）求點D的坐標；
  （3）拋物線上是否存在點K，使得以AC為邊的平行四邊形ACKL的面積等于△ABC的面積？若存在，請直接寫出點K的橫坐標；若不存在，請說明理由．[提示：拋物線y=ax²+bx+c（a≠0）的對稱軸為直線x=-

  b

  2

  a

  ，頂點坐標為（-

  b

  2

  a

  ，

  4

  ac

  -

  b

  2

  4

  a

  ）]．
  組卷：633引用：50難度：0.5

  解析

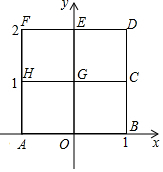• 6．如圖，2×2網格（每個小正方形的邊長為1）中，有A，O，B，C，D，E，F，H，G九個格點．拋物線l的解析式為y=

  1

  2

  x²+bx+c.
  （1）若l經過點O（0，0）和B（1，0），則b=

  ，c=

  ；它還經過的另一格點的坐標為

  ．
  （2）若l經過點H（-1，1）和G（0，1），求它的解析式及頂點坐標；通過計算說明點D（1，2）是否在l上．
  （3）若l經過這九個格點中的三個，直接寫出所有滿足這樣的拋物線的條數．
  組卷：338引用：52難度：0.5

  解析

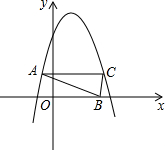• 7．如圖，在Rt△ABC中，∠C=90°，頂點A、C的坐標分別為（-1，2），（3，2），點B在x軸上，點B的坐標為（3，0），拋物線y=-x²+bx+c經過A、C兩點．
  （1）求該拋物線所對應的函數關系式；
  （2）點P是拋物線上的一點，當S_△PAB=

  5

  4

  S_△ABC時，求點P的坐標；
  （3）若點N由點B出發，以每秒

  6

  5

  個單位的速度沿邊BC、CA向點A移動，

  1

  3

  秒后，點M也由點B出發，以每秒1個單位的速度沿線段BO向點O移動，當其中一個點到達終點時另一個點也停止移動，點N的移動時間為t秒，當MN⊥AB時，請直接寫出t的值，不必寫出解答過程．
  組卷：584引用：52難度：0.5

  解析

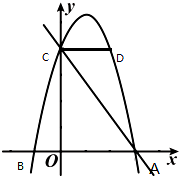• 8．如圖，平面直角坐標系中，拋物線y=ax²+bx+4經過點D（2，4），且與x軸交于A（3，0），B（-1，0）兩點，與y軸交于點C，連接AC，CD，BC
  （1）直接寫出該拋物線的解析式
  （2）點P是所求拋物線上的一個動點，過點P作x軸的垂線l,l分別交x軸于點E，交直線AC于點M．設點P的橫坐標為m.
  ①當0≤m≤2時，過點M作MG∥BC，MG交x軸于點G，連接GC，則m為何值時，△GMC的面積取得最大值，并求出這個最大值
  ②當-1≤m≤2時，試探求：是否存在實數m,使得以P，C，M為頂點的三角形和△AEM相似？若存在，求出相應的m值；若不存在，請說明理由．
  組卷：523引用：50難度：0.5

  解析

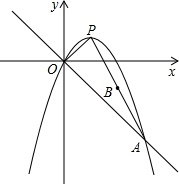• 9．如圖，已知直線y=-x與二次函數y=-x²+bx+c的圖象交于點A、O，O是坐標原點，OA=3

  2

  ，點P為二次函數圖象的頂點，點B是AP的中點．
  （1）求點A的坐標和二次函數的解析式；
  （2）求線段OB的長；
  （3）射線OB上是否存在點M，使得△AOM與△AOP相似？若存在，請求點M的坐標；若不存在，請說明理由．
  組卷：452引用：50難度：0.5

  解析

• 10．如圖，拋物線y=ax²+bx+c與坐標軸分別交于A（-3，0），B（1，0），C（0，3），D是拋物線頂點，E是對稱軸與x軸的交點
  （1）求拋物線解析式；
  （2）F是拋物線對稱軸上一點，且tan∠AFE=

  1

  2

  ，求點O到直線AF的距離；
  （3）點P是x軸上的一個動點，過P作PQ∥OF交拋物線于點Q，是否存在以點O，F，P，Q為頂點的平行四邊形？若存在，求出點P坐標；若不存在，請說明理由．
  組卷：694引用：50難度：0.5

  解析

三、解答題（共28小題）

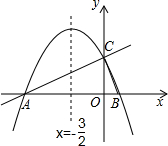• 29．如圖，在平面直角坐標系xOy中，直線y=

  1

  2

  x+2與x軸交于點A，與y軸交于點C．拋物線y=ax²+bx+c的對稱軸是直線x=-

  3

  2

  且經過A、C兩點，與x軸的另一交點為點B．
  （1）①直接寫出點B的坐標；
  ②求拋物線解析式．
  （2）若點P為直線AC上方的拋物線上的一點，連接PA，PC．求△PAC的面積的最大值，并求出此時點P的坐標．
  （3）拋物線上是否存在點M，過點M作MN垂直x軸于點N，使得以點A、M、N為頂點的三角形與△ABC相似？若存在，求出點M的坐標；若不存在，請說明理由．
  組卷：15765引用：81難度：0.1

  解析

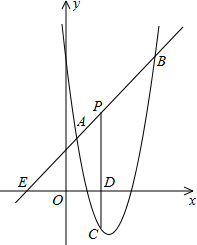• 30．如圖，直線y=x+2與拋物線y=ax²+bx+6（a≠0）相交于A（

  1

  2

  ，

  5

  2

  ）和B（4，m），點P是線段AB上異于A、B的動點，過點P作PC⊥x軸于點D，交拋物線于點C．
  （1）求拋物線的解析式；
  （2）是否存在這樣的P點，使線段PC的長有最大值？若存在，求出這個最大值；若不存在，請說明理由；
  （3）求△PAC為直角三角形時點P的坐標．
  組卷：30501引用：99難度：0.1

  解析