2022-2023學年山東省德州市寧津縣八年級（下）期末數學試卷

一、選擇題：本大題共12小題，在每小題給出的四個選項中，只有一項是正確的，

• 1．若二次根式

  x

  -

  6

  有意義，則x的取值范圍是（　　）

  A．x≥6

  B．x≥0

  C．x≥-6

  D．x≤6
  組卷：284引用：9難度：0.8

  解析

• 2．為了解美食節同學們最喜愛的菜肴，需要獲取的統計量是（　　）

  A．平均數

  B．中位數

  C．眾數

  D．方差
  組卷：238引用：6難度：0.7

  解析

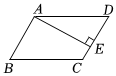• 3．如圖，在平行四邊形ABCD中，AE⊥CD于點E，∠B=65°，則∠DAE等于（　　）

  A．15°

  B．25°

  C．35°

  D．65°
  組卷：292引用：7難度：0.7

  解析

• 4．如圖，小紅家的木門左下角有一點受潮，她想檢測門是否變形，準備采用如下方法：先測量門的邊AB和BC的長，再測量點A和點C間的距離，由此可推斷∠B是否為直角，這樣做的依據是（　　）
  

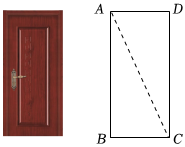
  A．勾股定理

  B．勾股定理的逆定理

  C．三角形內角和定理

  D．直角三角形的兩銳角互余
  組卷：1092引用：13難度：0.5

  解析

• 5．在同一坐標系中，函數y=kx與y=x-k的圖象大致是（　　）

  A．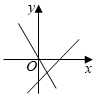

  B．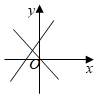

  C．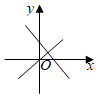

  D．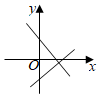
  組卷：3680引用：20難度：0.6

  解析

• 6．下列運算正確的是（　　）

  A． 2 + 3 = 5

  B． 2 × 8 = 16

  C． 6 ÷ 3 = 2

  D． （ - 3 ） 2 = - 3
  組卷：68引用：3難度：0.8

  解析

• 7．下列性質中，菱形具有而矩形不一定具有的是（　　）

  A．對邊相等	B．對角線互相平分
  C．鄰邊相等	D．對角線相等
  組卷：23引用：1難度：0.5

  解析

• 8．圖1是第七屆國際數學教育大會（ICME）會徽，在其主體圖案中選擇兩個相鄰的直角三角形，恰好能組合得到如圖2所示的四邊形OABC．若AB=BC=2，且∠AOB=30°，則OC的長度為（　　）

  A． 2 2

  B． 2 3

  C．4

  D． 2 5
  組卷：545引用：15難度：0.7

  解析

三、解答題：本大題共7小題，共78分.

• 24．勾股定理是人類早期發現并證明的重要數學定理之一，是用代數思想解決幾何問題的最重要的工具之一，也是數形結合的紐帶之一，它不但因證明方法層出不窮吸引著人們，更因為應用廣泛而使人入迷．
  （1）證明勾股定理
  據傳當年畢達哥拉斯借助如圖3所示的兩個圖驗證了勾股定理，請你說說其中的道理．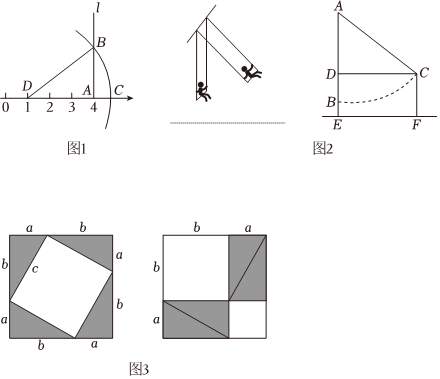
  
  （2）應用勾股定理
  ①應用場景1——在數軸上畫出表示無理數的點．
  如圖1，在數軸上找出表示4的點A，過點A作直線l垂直于DA，在l上取點B，使AB=2，以點D為圓心，DB為半徑作弧，則弧與數軸的交點C表示的數是

  ．
  ②應用場景2——解決實際問題．
  如圖2，鄭州某公園有一秋千，秋千靜止時，踏板離地的垂直高度BE=0.5m,將它往前推2m至C處時，水平距離CD=2m,踏板離地的垂直高度CF=1.5m,它的繩索始終拉直，求繩索AC的長．
  組卷：350引用：5難度：0.5

  解析

• 25．（1）對于試題“如圖①，在正方形ABCD中，E、F分別是BC、DC上的點，且∠EAF=45°，連接EF，探究BE、DF、EF之間的數量關系”，數學王老師給出了如下的思路：
  

  延長CB到M，使得BM=DF，連接AM，……，利用三角形全等的判定及性質解答，……

  請根據數學王老師的思路探究BE、DF、EF之間的數量關系，并說明理由；
  （2）如圖②，在四邊形ABCD中，AB=AD，∠B+∠D=180°，E、F分別是BC、DC上的點，且∠EAF=

  1

  2

  ∠BAD，此時（1）中的結論是否仍然成立？請說明理由．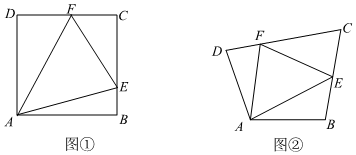
  
  組卷：478引用：4難度：0.5

  解析