人教五四新版九年級（下）中考題單元試卷：第34章 銳角三角函數（05）

一、選擇題（共2小題）

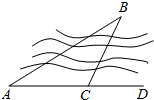• 1．如圖，要測量B點到河岸AD的距離，在A點測得∠BAD=30°，在C點測得∠BCD=60°，又測得AC=100米，則B點到河岸AD的距離為（　　）

  A．100米

  B．50 3 米

  C． 200 3 3 米

  D．50米
  組卷：3130引用：70難度：0.9

  解析

• 2．如圖，已知“人字梯”的5個踩檔把梯子等分成6份，從上往下的第二個踩檔與第三個踩檔的正中間處有一條60cm長的綁繩EF，tanα=

  5

  2

  ，則“人字梯”的頂端離地面的高度AD是（　　）

  A．144cm

  B．180cm

  C．240cm

  D．360cm
  組卷：3817引用：66難度：0.7

  解析

二、填空題（共3小題）

• 3．如圖，河流兩岸a、b互相平行，點A、B是河岸a上的兩座建筑物，點C、D是河岸b上的兩點，A、B的距離約為200米．某人在河岸b上的點P處測得∠APC=75°，∠BPD=30°，則河流的寬度約為
  組卷：2445引用：59難度：0.5

  解析

• 4．如圖1是小志同學書桌上的一個電子相框，將其側面抽象為如圖2所示的幾何圖形，已知BC=BD=15cm,∠CBD=40°，則點B到CD的距離為

  cm（參考數據sin20°≈0.342，cos20°≈0.940，sin40°≈0.643，cos40°≈0.766，結果精確到0.1cm,可用科學計算器）．
  組卷：2350引用：64難度：0.5

  解析

• 5．為解決停車難的問題，在如圖一段長56米的路段開辟停車位，每個車位是長5米寬2.2米的矩形，矩形的邊與路的邊緣成45°角，那么這個路段最多可以劃出

  個這樣的停車位．（

  2

  ≈1.4）
  組卷：2899引用：68難度：0.7

  解析

三、解答題（共25小題）

• 6．如圖，一條輸電線路從A地到B地需要經過C地，圖中AC=20千米，∠CAB=30°，∠CBA=45°，因線路整改需要，將從A地到B地之間鋪設一條筆直的輸電線路．
  （1）求新鋪設的輸電線路AB的長度；（結果保留根號）
  （2）問整改后從A地到B地的輸電線路比原來縮短了多少千米？（結果保留根號）
  組卷：1508引用：54難度：0.5

  解析

• 7．如圖，一條河的兩岸l₁，l₂互相平行，在一次綜合實踐活動中，小穎去測量這條河的寬度，先在對岸l₁上選取一個點A，然后在河岸l₂時選擇點B，使得AB與河岸垂直，接著沿河岸l₂走到點C處，測得BC=60米，∠BCA=62°，請你幫小穎算出河寬AB（結果精確到1米）．（參考數據：sin62°≈0.88，cos62°≈0.47，tan62°≈1.88）
  組卷：1062引用：56難度：0.7

  解析

• 8．如圖1所示的晾衣架，支架主視圖的基本圖形是菱形，其示意圖如圖2，晾衣架伸縮時，點G在射線DP上滑動，∠CED的大小也隨之發生變化，已知每個菱形邊長均等于20cm,且AH=DE=EG=20cm.
  （1）當∠CED=60°時，求C、D兩點間的距離；
  （2）當∠CED由60°變為120°時，點A向左移動了多少cm？（結果精確到0.1cm）
  （3）設DG=xcm,當∠CED的變化范圍為60°～120°（包括端點值）時，求x的取值范圍．（結果精確到0.1cm）（參考數據

  3

  ≈1.732，可使用科學計算器）
  
  組卷：984引用：57難度：0.5

  解析

• 9．如圖1，A，B，C是三個垃圾存放點，點B，C分別位于點A的正北和正東方向，AC=100米．四人分別測得∠C的度數如下表：
  

  	甲	乙	丙	丁
  ∠C（單位：度）	34	36	38	40

  他們又調查了各點的垃圾量，并繪制了下列尚不完整的統計圖2，圖3：
  
  （1）求表中∠C度數的平均數

  x

  ：
  （2）求A處的垃圾量，并將圖2補充完整；
  （3）用（1）中的

  x

  作為∠C的度數，要將A處的垃圾沿道路AB都運到B處，已知運送1千克垃圾每米的費用為0.005元，求運垃圾所需的費用．（注：sin37°=0.6，cos37°=0.8，tan37°=0.75）
  組卷：875引用：58難度：0.5

  解析

• 10．如圖，在水平地面上豎立著一面墻AB，墻外有一盞路燈D．光線DC恰好通過墻的最高點B，且與地面形成37°角．墻在燈光下的影子為線段AC，并測得AC=5.5米．
  （1）求墻AB的高度（結果精確到0.1米）；（參考數據：tan37°≈0.75，sin37°≈0.60，cos37°≈0.80）
  （2）如果要縮短影子AC的長度，同時不能改變墻的高度和位置，請你寫出兩種不同的方法．
  組卷：1703引用：54難度：0.5

  解析

三、解答題（共25小題）

• 29．為倡導“低碳生活”，人們常選擇以自行車作為代步工具、圖（1）所示的是一輛自行車的實物圖．圖（2）是這輛自行車的部分幾何示意圖，其中車架檔AC與CD的長分別為45cm和60cm,且它們互相垂直，座桿CE的長為20cm.點A、C、E在同一條直線上，且∠CAB=75°．（參考數據：sin75°=0.966，cos75°=0.259，tan75°=3.732）
  
  （1）求車架檔AD的長；
  （2）求車座點E到車架檔AB的距離（結果精確到1cm）．
  組卷：1489引用：71難度：0.5

  解析

• 30．解放橋是天津市的標志性建筑之一，是一座全鋼結構的部分可開啟的橋梁．
  （Ⅰ）如圖①，已知解放橋可開啟部分的橋面的跨度AB等于47m,從AB的中點C處開啟，則AC開啟至AC′的位置時，AC′的長為

  m；
  （Ⅱ）如圖②，某校數學興趣小組要測量解放橋的全長PQ，在觀景平臺M處測得∠PMQ=54°，沿河岸MQ前行，在觀景平臺N處測得∠PNQ=73°，已知PQ⊥MQ，MN=40m,求解放橋的全長PQ（tan54°≈1.4，tan73°≈3.3，結果保留整數）．
  
  組卷：1755引用：56難度：0.3

  解析