2021-2022學年北京市海淀區三帆中學七年級(下)月考數學試卷(6月份)
發布:2024/4/20 14:35:0
一、選擇題(每小題2分,共16分)
-
1.點A(-2,-3)所在象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限 組卷:155引用:10難度:0.9 -
2.下列各數中的無理數是( )
A. 27B. 227C.3. ?4D. (3)2組卷:115引用:2難度:0.9 -
3.下列事件中,調查方式選擇合理的是( )
A.為了解某批智能手機操作系統的性能,選擇全面調查 B.為了解北京市某年齡段人群的網購意向,選擇全面調查 C.為審查某文章中的錯別字,選擇抽樣調查 D.為了解某班學生的身高情況,選擇全面調查 組卷:74引用:1難度:0.7 -
4.已知a<b,下列不等式變形不正確的是( )
A.a+2<b+2 B.3a<3b C.-2a<-2b D.2a-1<2b-1 組卷:617引用:4難度:0.8 -
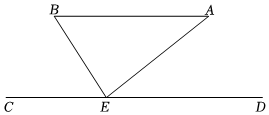 5.如圖,AB∥CD,點E在直線CD上,若∠B=57°,∠AED=38°,則∠AEB的度數為( )
5.如圖,AB∥CD,點E在直線CD上,若∠B=57°,∠AED=38°,則∠AEB的度數為( )A.38° B.57° C.85° D.95° 組卷:92引用:7難度:0.6 -
6.如圖,將北京市地鐵部分線路圖置于正方形網格中,若崇文門站的坐標為(0,-1),西單站的坐標為(-5,0),則雍和宮站的坐標為( )
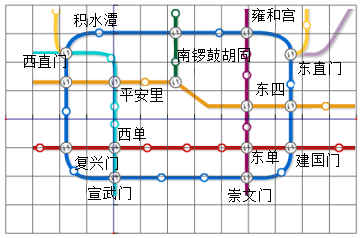
A.(4,0) B.(-4,0) C.(0,-4) D.(0,4) 組卷:209引用:2難度:0.7 -
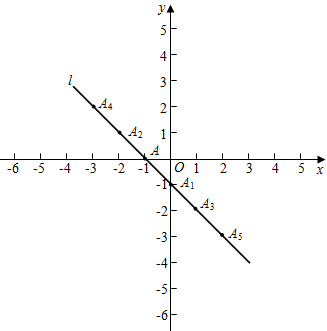 7.在平面直角坐標系xOy中,直線l經過點A(-1,0),點A1,A2,A3,A4,A5,……按如圖所示的規律排列在直線l上.若直線l上任意相鄰兩個點的橫坐標都相差1,縱坐標也都相差1,若點An(為正整數)的縱坐標為-2022,則n的值為( )
7.在平面直角坐標系xOy中,直線l經過點A(-1,0),點A1,A2,A3,A4,A5,……按如圖所示的規律排列在直線l上.若直線l上任意相鄰兩個點的橫坐標都相差1,縱坐標也都相差1,若點An(為正整數)的縱坐標為-2022,則n的值為( )A.4042 B.4043 C.4044 D.4045 組卷:194引用:1難度:0.7 -
8.從A地到B地有駕車、公交、地鐵三種出行方式,為了選擇適合的出行方式,對6:00-10:00時段這三種出行方式不同出發時刻所用時長(從A地到B地)進行調查、記錄與整理,數據如圖所示.
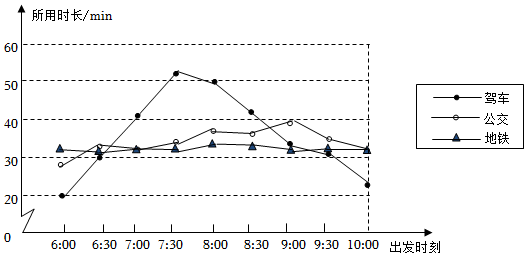
根據統計圖提供的信息,下列推斷合理的是( )A.若8:00出發,駕車是最快的出行方式 B.地鐵出行所用時長受出發時刻影響較小 C.若選擇公交出行且需要30分鐘以內到達,則7:30之前出發均可 D.同一時刻出發,不同出行方式所用時長的差最長可達30分鐘 組卷:810引用:10難度:0.8
四、選做題(共10分,每題5分)
-
25.在用計算機程序求一元方程的解時,常用“二分法”的算法思路.
借鑒這種思路,小明編寫了一個程序來求一個正數a的算術平方根.以a=10為例,要求,相當于求方程x2-10=0的正數解,他設計的程序是這樣的:10
第一步:輸入一個比小的正數L1,一個比10大的正數R1,則L12-10<0,R12-10>0.10
取M1=(L1+R1),計算M12-10,可能有以下三種結果:12
①如果M12-10=0,那么方程的解為M1,輸出結果,程序運行結束;
②如果M12-10<0,那么記L2=M1,R2=R1:
③如果M12-10>0,那么記L2=L1,R2=M1.
第二步:取M2=(L2+R2),計算M22-10,并根據M22-10與0的大小關系繼續為L3、R3賦值或輸出結果.12
第三步:取M3=(L3+R3),計算M32-10,……12
……
第N步:取Mn=(Ln+Rn),輸出方程的(近似)解Mn,程序運行結束.12
當程序求出方程的解,或者運行到指定的步數時(不能無限進行),均輸出結果,結束運行.
小明運行程序,當指定步數不超過4時,得到了下面的過程和結果:
(1)請補全如表中空缺的過程和結果;Li Ri Mi Mi2-10 i=1 輸入:3 輸入:4 >0 i=2 賦值:3 賦值: 3.25 0 i=3 賦值: 賦值:3.25 3.125 <0 i=4 賦值: 賦值: 輸出: /
(2)如果要計算23的算術平方根,在輸入L1=4,R1=5的情況下,請寫出程序運行兩步后的結果:M2=.組卷:83引用:1難度:0.5 -
26.在平面直角坐標系中,如果點P的坐標為(x,y),那么把點Q(kx,ky)(其中k≠0)稱為點P的“[k]位置點”.已知,點A(-1,2),B(3,2).
(1)若點A′,B′分別是點A,B的“[2]位置點”,則線段A′B′=;
(2)點M是線段AB上一點,點N是點M的一個“[k]位置點“.
①當M在線段AB上運動時,若點M,N之間的距離的最小值為5,求k的值;
②如圖,點E(-2,3),F(-2,6),G(-5,6),H(-5,3),如果在線段AB上能找到至少一個點M,使點N在正方形EFGH的內部或邊上,直接寫出k的取值范圍.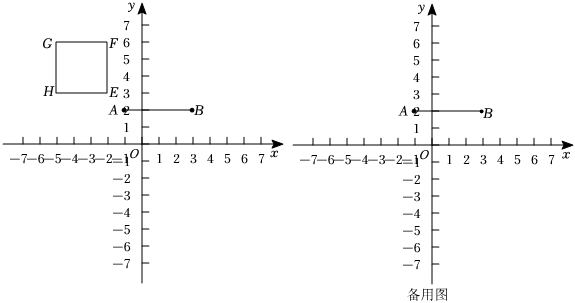 組卷:68引用:1難度:0.1
組卷:68引用:1難度:0.1


