人教五四新版九年級（上）中考題單元試卷：第28章 二次函數(shù)（04）

一、選擇題（共17小題）

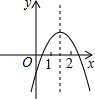• 1．二次函數(shù)y=ax²+bx+c（a≠0）的圖象如圖所示，下列結論：①2a+b＞0；②abc＜0；③b²-4ac＞0；④a+b+c＜0；⑤4a-2b+c＜0，其中正確的個數(shù)是（　　）

  A．2

  B．3

  C．4

  D．5
  組卷：3829引用：66難度：0.9

  解析

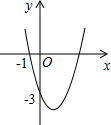• 2．如圖，拋物線y=ax²+bx+c（a≠0）過點（-1，0）和點（0，-3），且頂點在第四象限，設P=a+b+c,則P的取值范圍是（　　）

  A．-3＜P＜-1

  B．-6＜P＜0

  C．-3＜P＜0

  D．-6＜P＜-3
  組卷：9552引用：85難度：0.5

  解析

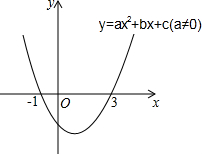• 3．二次函數(shù)y=ax²+bx+c（a≠0）的圖象如圖所示，下列說法：
  ①2a+b=0
  ②當-1≤x≤3時，y＜0
  ③若（x₁，y₁）、（x₂，y₂）在函數(shù)圖象上，當x₁＜x₂時，y₁＜y₂
  ④9a+3b+c=0
  其中正確的是（　　）

  A．①②④

  B．①④

  C．①②③

  D．③④
  組卷：3299引用：72難度：0.9

  解析

• 4．如圖，已知經過原點的拋物線y=ax²+bx+c（a≠0）的對稱軸是直線x=-1，下列結論中：①ab＞0，②a+b+c＞0，③當-2＜x＜0時，y＜0．正確的個數(shù)是（　　）

  A．0個

  B．1個

  C．2個

  D．3個
  組卷：2093引用：61難度：0.9

  解析

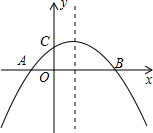• 5．如圖，二次函數(shù)y=ax²+bx+c（a≠0）的圖象與x軸交于A，B兩點，與y軸交于點C，且OA=OC．則下列結論：
  ①abc＜0；②

  b

  2

  -

  4

  ac

  4

  a

  ＞0；③ac-b+1=0；④OA?OB=-

  c

  a

  ．
  其中正確結論的個數(shù)是（　　）

  A．4

  B．3

  C．2

  D．1
  組卷：11908引用：98難度：0.9

  解析

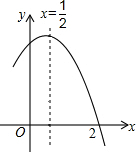• 6．如圖是二次函數(shù)y=ax²+bx+c（a≠0）圖象的一部分，對稱軸為直線x=

  1

  2

  ，且經過點（2，0），有下列說法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y₁），（1，y₂）是拋物線上的兩點，則y₁=y₂．上述說法正確的是（　　）

  A．①②④

  B．③④

  C．①③④

  D．①②
  組卷：4129引用：67難度：0.9

  解析

• 7．如圖，觀察二次函數(shù)y=ax²+bx+c的圖象，下列結論：
  ①a+b+c＞0，②2a+b＞0，③b²-4ac＞0，④ac＞0．
  其中正確的是（　　）

  A．①②

  B．①④

  C．②③

  D．③④
  組卷：2867引用：62難度：0.9

  解析

• 8．如圖，已知頂點為（-3，-6）的拋物線y=ax²+bx+c經過點（-1，-4），則下列結論中錯誤的是（　　）

  A．b2＞4ac

  B．ax2+bx+c≥-6

  C．若點（-2，m），（-5，n）在拋物線上，則m＞n

  D．關于x的一元二次方程ax2+bx+c=-4的兩根為-5和-1
  組卷：3727引用：79難度：0.9

  解析

• 9．已知二次函數(shù)y=ax²+bx+c（a≠0）的圖象如圖所示，對稱軸是直線x=-1，下列結論：
  ①abc＜0；②2a+b=0；③a-b+c＞0；④4a-2b+c＜0
  其中正確的是（　　）

  A．①②

  B．只有①

  C．③④

  D．①④
  組卷：4151引用：78難度：0.9

  解析

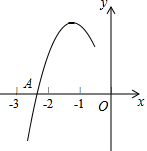• 10．拋物線y=ax²+bx+c（a≠0）的對稱軸為直線x=-1，與x軸的一個交點A在點（-3，0）和（-2，0）之間，其部分圖象如圖，則下列結論：①4ac-b²＜0；②2a-b=0；③a+b+c＜0；④點M（x₁，y₁）、N（x₂，y₂）在拋物線上，若x₁＜x₂，則y₁≤y₂，其中正確結論的個數(shù)是（　　）

  A．1個

  B．2個

  C．3個

  D．4個
  組卷：2593引用：65難度：0.9

  解析

三、解答題（共3小題）

• 29．已知拋物線y₁=ax²+bx+c（a≠0）與x軸相交于點A，B（點A，B在原點O兩側），與y軸相交于點C，且點A，C在一次函數(shù)y₂=

  4

  3

  x+n的圖象上，線段AB長為16，線段OC長為8，當y₁隨著x的增大而減小時，求自變量x的取值范圍．
  組卷：1076引用：53難度：0.5

  解析

• 30．在平面直角坐標系xOy中，拋物線y=mx²-2mx-2（m≠0）與y軸交于點A，其對稱軸與x軸交于點B．
  （1）求點A，B的坐標；
  （2）設直線l與直線AB關于該拋物線的對稱軸對稱，求直線l的解析式；
  （3）若該拋物線在-2＜x＜-1這一段位于直線l的上方，并且在2＜x＜3這一段位于直線AB的下方，求該拋物線的解析式．
  組卷：2134引用：59難度：0.5

  解析