免费av一区二区,综合激情五月婷婷,亚洲一区二区三区三

當前位置：章節挑題

請展開查看知識點列表

人教版：九年級下

教材版本: 人教版人教版（2024）北師大版北師大版（2024）華東師大版華東師大版（2024）蘇科版蘇科版（2024）湘教版湘教版（2024）青島版青島版（2024）浙教版浙教版（2024）冀教版冀教版（2024）滬科版滬科版（2024）魯教五四版魯教五四版（2024）北京課改版北京課改版（2024）滬教五四版滬教五四版（2024）人教五四版人教五四版（2024）

年級: 七年級上七年級下八年級上八年級下九年級上九年級下

第26章反比例函數
第27章相似
第28章銳角三角函數
第29章投影與視圖

更多>>

原創

更新中

《黃金講練》2024-2025學年人教版（2024）七下同步課堂

知識圖解新知探究答疑解惑針對訓練

瀏覽次數：6343 更新：2025年06月06日

原創

已完結

【解題模型】2024-2025學年人教版（2024）七下

解題模型因材施教夯實基礎穩步提升

瀏覽次數：13522 更新：2025年06月04日

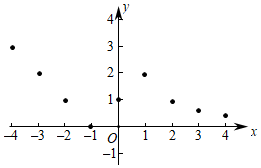2641．若一個函數當自變量在不同范圍內取值時，函數表達式不同，我們稱這樣的函數為分段函數，下面我們參照學習函數的過程與方法，探究分段函數y=
|
x
+
1
|
（
x
≤
1
）
2
x
（
x
＞
1
）
的圖象與性質，探究過程如下，請補充完整．
（1）列表：

x … -4 -3 -2 -1 0 1 2 3 4 …

y … 3 m 1 0 1 2 1 n
1
2
…

其中，m=
，n=
．
（2）描點：在平面直角坐標系中，以自變量x的取值為橫坐標，以相應的函數值y為縱坐標，描出相應的點，如圖所示，請畫出函數的圖象．
（3）研究函數并結合圖象與表格，回答下列問題：
①點A（
7
2
，y₁），B（5，y₂），C（x₁，
5
2
），D（x₂，6）在函數圖象上，則y₁
y₂，x₁
x₂；（填“＞”，“=”或“＜”）
②當函數值y=1時，求自變量x的值；
（4）若直線y=-x+b與函數圖象有且只有一個交點，請直接寫出b的取值范圍．

發布：2024/5/23 20:19:40組卷：837引用：15難度：0.6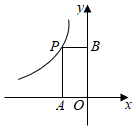

解析

2642．反比例函數y=-
5
x
（x＜0）的圖象如圖所示，則矩形OAPB的面積是
．
發布：2024/5/23 20:19:40組卷：974引用：10難度：0.9
解析
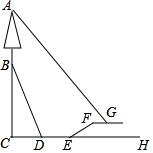2643．我校數學社團學生小明想測量學校對面斜坡BD上的信號樹AB的高度，已知BD的坡度為1：
5
12
，且BD的長度為65米，小明從坡底D處沿直線走到學校大臺階底部E處，DE長為20米，他沿著與水平地面成30°夾角的大臺階行走20米到達平臺F處，又向前走了13米到達平臺上的旗桿G處，此時他仰望信號樹的頂部A，測得仰角為50°，則信號樹AB的高度約為（　　）（小明的身高忽略不計）
（參考數據：
2
≈1.4，
3
≈1.7，sin50°≈0.77，cos50°≈0.64，tan50°≈1.2）
A．45米 B．30米 C．35米 D．40米
發布：2024/5/23 20:19:40組卷：406引用：5難度：0.5
解析
2644．一個長方體的三視圖如圖所示，若其俯視圖為正方形，則這個長方體的表面積為（　　）
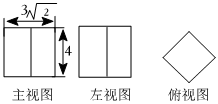
A．50 B．66 C．70 D．76
發布：2024/5/23 20:19:40組卷：43引用：4難度：0.6
解析
2645．如圖，請在圖2中畫出與圖1相似的縮小圖形．
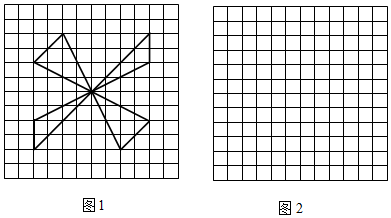發布：2024/5/23 20:19:40組卷：4引用：2難度：0.5
解析
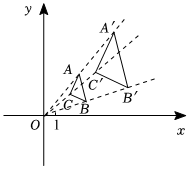2646．如圖，在平面直角坐標系中，△ABC和△A′B′C′是以坐標原點O為位似中心的位似圖形，且點B（3，1），B′（6，2），若點A′（5，6），則A的坐標為
．
發布：2024/5/23 20:19:40組卷：599引用：8難度：0.7
解析
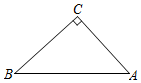2647．如圖，在△ABC中，∠C=90°，∠B=42°，BC=8，若用科學計算器求AC的長，則下列按鍵順序正確的是（　　）
A． B．
C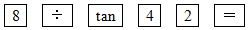． D．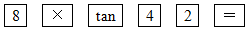
發布：2024/5/23 20:19:40組卷：1149引用：7難度：0.6
解析
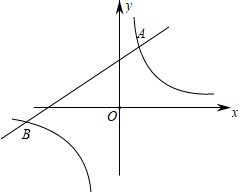2648．如圖，一次函數y=kx+b（k≠0）的圖象與反比例函數y=
m
x
（m≠0）的圖象相交于點A（2，3），B（-6，-1），則關于x的不等式kx+b＞
m
x
的解集是（　　）
A．x＞-6 B．-6＜x＜0
C．-6＜x＜0且x＞2 D．-6＜x＜0或x＞2
發布：2024/5/23 20:19:40組卷：1403引用：4難度：0.6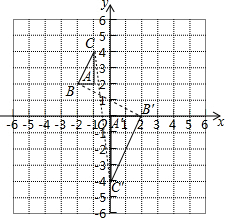
解析
2649．△ABC與△A′B′C′位似，且A（-1，2），B（-2，2），C（-1，4），A′（0，0），B′（2，0），C′（0，-4），畫出位似中心，并寫出△ABC與△A′B′C′的位似比．
發布：2024/5/23 20:19:40組卷：295引用：4難度：0.7
解析
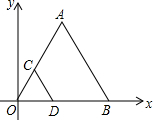2650．如圖，線段CD兩個端點的坐標分別為C（1，2），D（2，0），以原點為位似中心，將線段CD放大得到線段AB，若點B的坐標為（6，0），則點A的坐標為（　　）
A．（2，5） B．（2.5，5） C．（3，5） D．（3，6）
發布：2024/5/23 20:19:40組卷：815引用：14難度：0.9
解析

首頁上一頁 …265 266 267 268 …下一頁尾頁

A．x＞-6	B．-6＜x＜0
C．-6＜x＜0且x＞2	D．-6＜x＜0或x＞2

A．	B．
C．	D．

2642．反比例函數y=-5x（x＜0）的圖象如圖所示，則矩形OAPB的面積是．

2644．一個長方體的三視圖如圖所示，若其俯視圖為正方形，則這個長方體的表面積為（ ）

2645．如圖，請在圖2中畫出與圖1相似的縮小圖形．

2646．如圖，在平面直角坐標系中，△ABC和△A′B′C′是以坐標原點O為位似中心的位似圖形，且點B（3，1），B′（6，2），若點A′（5，6），則A的坐標為 ．

2647．如圖，在△ABC中，∠C=90°，∠B=42°，BC=8，若用科學計算器求AC的長，則下列按鍵順序正確的是（ ）

2648．如圖，一次函數y=kx+b（k≠0）的圖象與反比例函數y=mx（m≠0）的圖象相交于點A（2，3），B（-6，-1），則關于x的不等式kx+b＞mx的解集是（ ）

2649．△ABC與△A′B′C′位似，且A（-1，2），B（-2，2），C（-1，4），A′（0，0），B′（2，0），C′（0，-4），畫出位似中心，并寫出△ABC與△A′B′C′的位似比．

2650．如圖，線段CD兩個端點的坐標分別為C（1，2），D（2，0），以原點為位似中心，將線段CD放大得到線段AB，若點B的坐標為（6，0），則點A的坐標為（ ）

2642．反比例函數y=-
5
x
（x＜0）的圖象如圖所示，則矩形OAPB的面積是
．

2644．一個長方體的三視圖如圖所示，若其俯視圖為正方形，則這個長方體的表面積為（　　）

2646．如圖，在平面直角坐標系中，△ABC和△A′B′C′是以坐標原點O為位似中心的位似圖形，且點B（3，1），B′（6，2），若點A′（5，6），則A的坐標為
．

2647．如圖，在△ABC中，∠C=90°，∠B=42°，BC=8，若用科學計算器求AC的長，則下列按鍵順序正確的是（　　）

2648．如圖，一次函數y=kx+b（k≠0）的圖象與反比例函數y=
m
x
（m≠0）的圖象相交于點A（2，3），B（-6，-1），則關于x的不等式kx+b＞
m
x
的解集是（　　）

2650．如圖，線段CD兩個端點的坐標分別為C（1，2），D（2，0），以原點為位似中心，將線段CD放大得到線段AB，若點B的坐標為（6，0），則點A的坐標為（　　）