當前位置：試卷中心 > 試卷詳情

2023-2024學年廣東四校聯考高三（上）月考數學試卷（9月份）（一）

發布：2025/6/28 22:0:13

一、單選題。本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

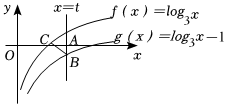1．如圖，直線x=t與函數f（x）=log₃x和g（x）=log₃x-1的圖象分別交于點A，B，若函數y=f（x）的圖象上存在一點C，使得△ABC為等邊三角形，則t的值為（　　）
A．
3
+
2
2
B．
3
3
+
3
2
C．
3
3
+
3
4
D．
3
3
+
3
組卷：540引用：4難度：0.5
解析
2．高斯是德國著名的數學家，近代數學奠基者之一，享有“數學王子”的美譽．函數f（x）=[x]稱為高斯函數，其中x∈R，[x]表示不超過x的最大整數，例如：[-1.1]=-2，[2.5]=2，則方程[2x+1]+[x]=4x的所有解之和為（　　）
A．
1
2
B．
3
4
C．
3
2
D．
7
4
組卷：235引用：9難度：0.5
解析
3．已知函數
f
（
x
）
=
sinπx
,
0
≤
x
≤
1
log
2023
x
,
x
＞
1
，若實數a,b,c互不相等，且f（a）=f（b）=f（c），則a+b+c的取值范圍是（　　）
A．（2，2024） B．（2，2024] C．（2，2023） D．（2，2023]
組卷：77引用：5難度：0.6
解析
4．“函數
f
（
x
）
=
lg
（
x
2
-
ax
+
1
2
）
在（1，+∞）上單調遞增”的一個充分不必要條件是（　　）
A．a≤2 B．
a
≤
3
2
C．
3
2
＜
a
＜
2
D．0≤a≤1
組卷：66引用：4難度：0.5
解析
5．已知e是自然對數的底數，
a
=
lo
g
2022
2
e
，
b
=
（
2
e
）
2022
，
c
=
202
2
2
c
，則（　　）
A．c＜a＜b B．a＜c＜b C．b＜a＜c D．a＜b＜c
組卷：24引用：3難度：0.6
解析
6．設等差數列{a_n}的前n項和為S_n，若S₃=16，S₆=8，則S₁₂=（　　）
A．-50 B．-60 C．-70 D．-80
組卷：399引用：5難度：0.7
解析
7．設全集U=I，M={x|y=ln（1-x）}，N={x|2^x（x-2）＜1}，則圖中陰影部分表示的集合為（　　）
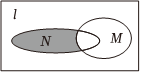
A．{x|x≥1} B．{x|1≤x＜2} C．{x|0＜x≤1} D．{x|x≤1}
組卷：29引用：13難度：0.9
解析
8．系統找不到該試題

二、多選題。本題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求。全部選對得5分，部分選對的得2分，有選錯的得0分。

9．設函數f（x）=2^x，對于任意的x₁，x₂（x₁≠x₂），下列命題中正確的是（　　）
A．f（x₁+x₂）=f（x₁）?f（x₂）
B．f（x₁?x₂）=f（x₁）+f（x₂）
C．
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
＞
0
D．
f
（
x
1
+
x
2
2
）
＜
f
（
x
1
）
+
f
（
x
2
）
2
組卷：2094引用：16難度：0.5
解析
10．已知數列{a_n}滿足a_n+a_n+1=2×（-1）ⁿ，n∈N^*，且a₅=1，則（　　）
A．a₁=-7
B．數列{a_2n-1}是等比數列
C．數列{|a_n|}是等差數列
D．數列
{
1
a
n
a
n
+
1
}
的前n項和為
n
14
n
-
49
組卷：26引用：2難度：0.5
解析

11．若函數f（x）滿足：①?x∈R，恒有f（x+2）=f（x-2）②?x∈R，恒有f（2-x）=f（x），③x∈[-1，1]時，f（x）=（x+1）²-1，則下列結論正確的是（　　）

A．f（22）=0

B．|f（x₂）-f（x₁）|的最大值為4

C．f（x）的單調遞減區間為[2k+1，2k+3]，k∈Z

D．若曲線y=k|x-1|-1與f（x）的圖象有6個不同的交點，則實數k的取值范圍為（

，1）

組卷：60引用：5難度：0.5

解析

12．已知函數f（x）滿足f（2-x）=f（x）=f（x-2），當x∈[-1，0]時，f（x）=2^x+1-1，g（x）=lg（|x|+1），則下列結論正確的是（　　）

A．?n∈Z，P（2n-1，0），f（x）上存在兩點M，N，使得△PMN是正三角形

B．?n∈Z，Q（2n,0），f（x）上存在兩點M，N，使得△QMN是正三角形

C．方程f（x）=x+b在區間[-1，2]上有兩根，則b的值有4個

D．當a為奇數和a為偶數時，函數h（x）=f（x）-g（x+a）的零點個數分別為m,n,則m-n是定值

組卷：17引用：2難度：0.6

解析

三、填空題。本題共4小題，每小題5分，共20分。

13．函數f（x）=x²+ax+5對x∈R恒有f（-2+x）=f（-2-x），若x∈[m,0]（m＜0）時，f（x）的值域為[1，5]，則實數m的取值范圍是
．
組卷：31引用：2難度：0.7
解析
14．函數
f
（
x
）
=
x
2
+
ax
+
4
a
x
+
16
x
2
-
8
，x∈（1，4]，|f（x）|最大值為M（a），則M（a）的最小值是
．
組卷：72引用：1難度：0.5
解析
15．偶函數f（x）在[0，+∞）上是減函數，則f（-4）
f（a²+4）（a∈R）．（填：＞、＜、≥、≤）
組卷：24引用：1難度：0.8
解析
16．設a₁，a₂，…a₁₀成等比數列，且a₁a₂…a₁₀=32，記x=a₁+a₂+…+a₁₀，y=
1
a
1
+
1
a
2
+…+
1
a
10
，則
x
y
=

．
組卷：85引用：3難度：0.5
解析

四、解答題。本題共6小題，共70分。解答應寫出必要的文字說明，證明過程或演算步驟。

17．某地政府指導本地建扶貧車間、搭建就業平臺，幫助貧困群眾實現精準脫貧，實現困難群眾就地就近就業．已知扶貧車間生產某種產品的年固定成本為8萬元，每生產x（x＞0）萬件，該產品需另投入流動成本W萬元．在年產量不足6萬件時，
W
=
1
2
x
2
+
x
；在年產量不小于6萬件時，
W
=
7
x
+
81
x
-
40
．每件產品的售價為6元．由于該扶貨車間利用了扶貧政策及企業產業鏈優勢，因此該種產品能在當年全部售完．
（1）寫出年利潤P（萬元）關于年產量x（萬件）的函數解析式；
（2）當年產量為多少時，該扶貧車間的年利潤最大？并求出最大年利潤．
組卷：71引用：4難度：0.5
解析
18．已知數列{a_n}是等差數列，其前n項和為A_n，a₇=15，A₇=63；數列{b_n}的前n項和為B_n，2B_n=3b_n-3（n∈N*）．
（Ⅰ）求數列{a_n}，{b_n}的通項公式；
（Ⅱ）求數列{
1
A
n
}的前n項和S_n；
（Ⅲ）求證：
n
∑
k
=
1
a
k
B
k
＜2．
組卷：858引用：6難度：0.5
解析
19．已知函數f（x）=lg（x+2）-lg（2-x）．
（1）求f（x）的定義域；
（2）判斷f（x）的奇偶性并予以證明；
（3）求不等式f（x）＞1的解集．
組卷：464引用：19難度：0.3
解析
20．閱讀材料，完成相應任務：“賈憲三角”又稱“楊輝三角”，在歐洲則稱為“帕斯卡三角”（如圖所示），它揭示了（a+b）ⁿ（n為非負數）展開式的各項系數的規律．

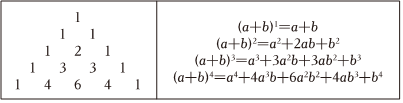
根據上述規律，完成下列問題：
（1）直接寫出（a+b）⁵=_____．
（2）（a+1）⁸的展開式中a項的系數是_____．
（3）利用上述規律求11⁵的值，寫出過程．
組卷：22引用：1難度：0.8
解析
21．.已知函數f（x）=lnx-x+1，x∈（0，+∞），g（x）=sinx-ax（a∈R）．
（1）求f（x）的最大值；
（2）若對?x₁∈（0，+∞），總存在
x
2
∈
（
0
，
π
2
）
，使得f（x₁）＜g（x₂）成立，求實數a的取值范圍；
（3）證明不等式
sin
（
1
n
）
n
+
sin
（
2
n
）
n
+
…
+
sin
（
n
n
）
n
＜
e
e
-
1
（其中e是自然對數的底數）．
組卷：335引用：3難度：0.2
解析
22．已知函數
f
（
x
）
=
2
e
x
e
x
+
1
+
k
是奇函數．（e是自然對數的底）
（1）求實數k的值；
（2）若x＞0時，關于x的不等式f（2x）≤mf（x）恒成立．求實數m的取值范圍；
（3）設
g
（
x
）
=
f
（
x
）
+
1
1
-
f
（
x
）
，對任意實數a,b,c∈（0，n]，若以a,b,c為長度的線段可以構成三角形時，均有以g（a），g（b），g（c）為長度的線段也能構成三角形，求實數n的最大值．
組卷：351引用：12難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

2023-2024學年廣東四校聯考高三（上）月考數學試卷（9月份）（一）

一、單選題。本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．如圖，直線x=t與函數f（x）=log3x和g（x）=log3x-1的圖象分別交于點A，B，若函數y=f（x）的圖象上存在一點C，使得△ABC為等邊三角形，則t的值為（ ）

2．高斯是德國著名的數學家，近代數學奠基者之一，享有“數學王子”的美譽．函數f（x）=[x]稱為高斯函數，其中x∈R，[x]表示不超過x的最大整數，例如：[-1.1]=-2，[2.5]=2，則方程[2x+1]+[x]=4x的所有解之和為（ ）

3．已知函數f（x）=sinπx,0≤x≤1log2023x,x＞1，若實數a,b,c互不相等，且f（a）=f（b）=f（c），則a+b+c的取值范圍是（ ）

4．“函數f（x）=lg（x2-ax+12）在（1，+∞）上單調遞增”的一個充分不必要條件是（ ）

5．已知e是自然對數的底數，a=log20222e，b=（2e）2022，c=20222c，則（ ）

6．設等差數列{an}的前n項和為Sn，若S3=16，S6=8，則S12=（ ）

7．設全集U=I，M={x|y=ln（1-x）}，N={x|2x（x-2）＜1}，則圖中陰影部分表示的集合為（ ）

二、多選題。本題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求。全部選對得5分，部分選對的得2分，有選錯的得0分。

9．設函數f（x）=2x，對于任意的x1，x2（x1≠x2），下列命題中正確的是（ ）

10．已知數列{an}滿足an+an+1=2×（-1）n，n∈N*，且a5=1，則（ ）

11．若函數f（x）滿足：①?x∈R，恒有f（x+2）=f（x-2）②?x∈R，恒有f（2-x）=f（x），③x∈[-1，1]時，f（x）=（x+1）2-1，則下列結論正確的是（ ）

12．已知函數f（x）滿足f（2-x）=f（x）=f（x-2），當x∈[-1，0]時，f（x）=2x+1-1，g（x）=lg（|x|+1），則下列結論正確的是（ ）

三、填空題。本題共4小題，每小題5分，共20分。

13．函數f（x）=x2+ax+5對x∈R恒有f（-2+x）=f（-2-x），若x∈[m,0]（m＜0）時，f（x）的值域為[1，5]，則實數m的取值范圍是．

14．函數f（x）=x2+ax+4ax+16x2-8，x∈（1，4]，|f（x）|最大值為M（a），則M（a）的最小值是 ．

15．偶函數f（x）在[0，+∞）上是減函數，則f（-4）f（a2+4）（a∈R）．（填：＞、＜、≥、≤）

16．設a1，a2，…a10成等比數列，且a1a2…a10=32，記x=a1+a2+…+a10，y=1a1+1a2+…+1a10，則xy= ．

四、解答題。本題共6小題，共70分。解答應寫出必要的文字說明，證明過程或演算步驟。

18．已知數列{an}是等差數列，其前n項和為An，a7=15，A7=63；數列{bn}的前n項和為Bn，2Bn=3bn-3（n∈N*）．（Ⅰ）求數列{an}，{bn}的通項公式；（Ⅱ）求數列{1An}的前n項和Sn；（Ⅲ）求證：n∑k=1akBk＜2．

19．已知函數f（x）=lg（x+2）-lg（2-x）．（1）求f（x）的定義域；（2）判斷f（x）的奇偶性并予以證明；（3）求不等式f（x）＞1的解集．

1．如圖，直線x=t與函數f（x）=log₃x和g（x）=log₃x-1的圖象分別交于點A，B，若函數y=f（x）的圖象上存在一點C，使得△ABC為等邊三角形，則t的值為（　　）

2．高斯是德國著名的數學家，近代數學奠基者之一，享有“數學王子”的美譽．函數f（x）=[x]稱為高斯函數，其中x∈R，[x]表示不超過x的最大整數，例如：[-1.1]=-2，[2.5]=2，則方程[2x+1]+[x]=4x的所有解之和為（　　）

3．已知函數
f
（
x
）
=
sinπx
,
0
≤
x
≤
1
log
2023
x
,
x
＞
1
，若實數a,b,c互不相等，且f（a）=f（b）=f（c），則a+b+c的取值范圍是（　　）

4．“函數
f
（
x
）
=
lg
（
x
2
-
ax
+
1
2
）
在（1，+∞）上單調遞增”的一個充分不必要條件是（　　）

5．已知e是自然對數的底數，
a
=
lo
g
2022
2
e
，
b
=
（
2
e
）
2022
，
c
=
202
2
2
c
，則（　　）

6．設等差數列{a_n}的前n項和為S_n，若S₃=16，S₆=8，則S₁₂=（　　）

7．設全集U=I，M={x|y=ln（1-x）}，N={x|2^x（x-2）＜1}，則圖中陰影部分表示的集合為（　　）

9．設函數f（x）=2^x，對于任意的x₁，x₂（x₁≠x₂），下列命題中正確的是（　　）

10．已知數列{a_n}滿足a_n+a_n+1=2×（-1）ⁿ，n∈N^*，且a₅=1，則（　　）

11．若函數f（x）滿足：①?x∈R，恒有f（x+2）=f（x-2）②?x∈R，恒有f（2-x）=f（x），③x∈[-1，1]時，f（x）=（x+1）²-1，則下列結論正確的是（　　）

12．已知函數f（x）滿足f（2-x）=f（x）=f（x-2），當x∈[-1，0]時，f（x）=2^x+1-1，g（x）=lg（|x|+1），則下列結論正確的是（　　）

13．函數f（x）=x²+ax+5對x∈R恒有f（-2+x）=f（-2-x），若x∈[m,0]（m＜0）時，f（x）的值域為[1，5]，則實數m的取值范圍是
．

14．函數
f
（
x
）
=
x
2
+
ax
+
4
a
x
+
16
x
2
-
8
，x∈（1，4]，|f（x）|最大值為M（a），則M（a）的最小值是
．

15．偶函數f（x）在[0，+∞）上是減函數，則f（-4）
f（a²+4）（a∈R）．（填：＞、＜、≥、≤）

16．設a₁，a₂，…a₁₀成等比數列，且a₁a₂…a₁₀=32，記x=a₁+a₂+…+a₁₀，y=
1
a
1
+
1
a
2
+…+
1
a
10
，則
x
y
=

．

18．已知數列{a_n}是等差數列，其前n項和為A_n，a₇=15，A₇=63；數列{b_n}的前n項和為B_n，2B_n=3b_n-3（n∈N*）．
（Ⅰ）求數列{a_n}，{b_n}的通項公式；
（Ⅱ）求數列{
1
A
n
}的前n項和S_n；
（Ⅲ）求證：
n
∑
k
=
1
a
k
B
k
＜2．

19．已知函數f（x）=lg（x+2）-lg（2-x）．
（1）求f（x）的定義域；
（2）判斷f（x）的奇偶性并予以證明；
（3）求不等式f（x）＞1的解集．