當前位置：試卷中心 > 試卷詳情

2021-2022學年河南省開封市五縣高一（上）期末數學試卷

發布：2025/6/29 12:0:14

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的。

1．下列四組函數中，f（x）與g（x）相等的是（　　）
A．f（x）=lnx²，g（x）=2lnx
B．
f
（
x
）
=
x
,
g
（
x
）
=
（
x
）
2
C．f（x）=x-1，g（x）=
x
2
-
1
x
+
1
D．f（x）=x,g（x）=log_aa^x（a＞0且a≠1）
組卷：5引用：1難度：0.8
解析
2．函數f（x）=2lnx+x-6的零點所在區間為（　　）
A．（1，2） B．（2，3） C．（3，4） D．（4，5）
組卷：194引用：3難度：0.7
解析
3．已知命題p：“?x≥0，x²-x+1≥0”，則它的否定為（　　）
A．?x＜0，x²-x+1＜0 B．?x＜0，x²-x+1＜0
C．?x≥0，x²-x+1＜0 D．?x≥0，x²-x+1＜0
組卷：256引用：13難度：0.9
解析
4．要得到函數y=
2
cosx的圖象，只需將函數y=
2
sin（x+
π
4
）的圖象（　　）
A．向左平移
π
4
個單位 B．向右平移
π
4
個單位
C．向上平移
π
4
個單位 D．向下平移
π
4
個單位
組卷：220引用：3難度：0.7
解析
5．若函數y=
a
-
sinx
的定義域為R，則實數a的取值范圍為（　　）
A．（-∞，-1] B．（-∞，1] C．[-1，+∞） D．[1，+∞）
組卷：29引用：0難度：0.7
解析
6．下列函數中，既是偶函數，又在區間（1，2）內是增函數的為（　　）
A．y=cos2x,x∈R B．y=x³+1，x∈R
C．y=
e
x
-
e
-
x
2
，x∈R D．y=log₂|x|，x∈R且x≠0
組卷：64引用：3難度：0.9
解析
7．設
a
=
lo
g
2
3
，
b
=
lo
g
4
5
，
c
=
2
-
0
.
1
，則a,b,c的大小關系為（　　）
A．a＞b＞c B．b＞a＞c C．c＞b＞a D．a＞c＞b
組卷：473引用：2難度：0.7
解析
8．已知x＞0，y＞0，且2x+y=xy,則x+2y的最小值為（　　）
A．8 B．9 C．
8
2
D．
9
2
組卷：246引用：4難度：0.7
解析
9．已知集合A={x∈N^*|1≤x≤10}，集合B={x|x²-9x+8≥0}，則A∩B=（　　）
A．{0，1，8，9，10} B．{1，8，9，10}
C．{x|8≤x≤10} D．{x|8≤x≤10或x=1}
組卷：66引用：2難度：0.9
解析
10．設x∈R，則“-2＜x＜2”是“1＜x＜2”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充要條件 D．既不充分也不必要條件
組卷：251引用：4難度：0.9
解析
11．若集合
A
=
{
x
|
y
=
x
}
，B={x|x²-x-2＜0}，則A∩B=（　　）
A．{x|0＜x＜1} B．{x|0≤x＜1} C．{x|0＜x＜2} D．{x|0≤x＜2}
組卷：15引用：5難度：0.8
解析
12．系統找不到該試題

二、填空題：本題共4小題，每小題5分，共20分。

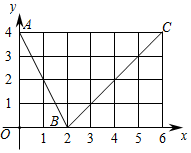13．如圖所示，函數f（x）的圖象是折線段ABC，其中A，B，C的坐標分別為（0，4），（2，0），（6，4），則f（f（0））=
．（用數字作答）
組卷：129引用：31難度：0.5
解析
14．（1）計算：7
lo
g
7
6
?
lo
g
6
5
?
lo
g
5
4
=
；
（2）已知lg2=a,lg3=b,那么log₅12=
．
組卷：92引用：2難度：0.7
解析
15．函數f（x）=
2
x
+
5
的定義域為
，值域為
．
組卷：20引用：1難度：0.7
解析
16．記min{x,y,z}表示x,y,z中的最小值，設函數f（x）=min{x,x²-4x+4，-2x+12}，則f（x）的最大值為
，f（x）≥1的解集為
．
組卷：55引用：2難度：0.8
解析

三、解答題：共70分.解答應寫出文字說明，證明過程或演算步驟。

17．已知函數
f
（
x
）
=
（
1
-
a
）
x
-
1
2
，
x
＜
0
a
x
2
+
2
x
-
a
,
x
≥
0
．
（1）若f（x）在R上單調遞增，求實數a的取值范圍；
（2）求f（x）在區間[1，2]上的最大值．
組卷：70引用：2難度：0.5
解析
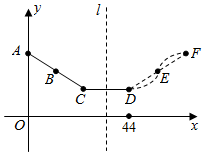18．在股票市場上，投資者常根據股價（每股的價格）走勢圖來操作，股民老張在研究某只股票時，發現其在平面直角坐標系內的走勢圖有如下特點：每日股價y（元）與時間x（天）的關系在ABC段可近似地用函數y=asin（ωx+φ）+20（a＞0，ω＞0，0＜φ＜π）的圖象從最高點A到最低點C的一段來描述（如圖），并且從C點到今天的D點在底部橫盤整理，今天也出現了明顯的底部結束信號．
老張預測這只股票未來一段時間的走勢圖會如圖中虛線DEF段所示，且DEF段與ABC段關于直線l：x=34對稱，點B、D的坐標分別是（12，20）、（44，12）．
（1）請你幫老張確定a、ω、φ的值，寫出ABC段的函數表達式，并指出此時x的取值范圍；
（2）請你幫老張確定虛線DEF段的函數表達式，并指出此時x的取值范圍；
（3）如果老張預測準確，且在今天買入該只股票，那么最短買入多少天后，股價至少是買入價的兩倍？
組卷：170引用：5難度：0.6
解析
19．倡導健康生活，推進全民健身，某社區去年購進A，B兩種健身器材若干件，經了解，B種健身器材的單價是A種健身器材的1.5倍，用7200元購買A種健身器材比用5400元購買B種健身器材多10件．
（1）A，B兩種健身器材的單價分別是多少元？
（2）若今年兩種健身器材的單價和去年保持不變，該社區計劃再購進A，B兩種健身器材共50件，且費用不超過21000元，請問：A種健身器材至少要購買多少件？
組卷：9引用：1難度：0.5
解析
20．求cos105°的值．
組卷：1引用：1難度：0.7
解析
21．已知函數f（x），g（x）分別是定義在R上的偶函數和奇函數，且f（x）+g（x）=x²-x+1．
（1）求函數f（x）與g（x）的解析式；
（2）設函數G（x）=f（x）+a|g（x）+1|，若對任意實數x,
G
（
x
）
≥
3
2
恒成立，求實數a的取值范圍．
組卷：173引用：3難度：0.4
解析
22．已知函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）
+
B
，
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
的一系列對應值如下表：

x -
π
6

π
3

5
π
6

4
π
3

11
π
6

7
π
3

17
π
6

y -1 1 3 1 -1 1 3

（1）根據表格提供的數據求函數f（x）的一個解析式；
（2）求函數f（x）的對稱中心及單調遞增區間；
（3）若對任意的實數a,函數y=f（kx）（k＞0），x∈
（
a
,
a
+
2
π
3
]
的圖象與直線y=1有且僅有兩個不同的交點，又當x∈[0，
π
3
]時，方程f（kx）=m恰有兩個不同的解，求實數m的取值范圍．
組卷：118引用：1難度：0.1
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．?x＜0，x²-x+1＜0	B．?x＜0，x²-x+1＜0
C．?x≥0，x²-x+1＜0	D．?x≥0，x²-x+1＜0

A．向左平移 π 4 個單位	B．向右平移 π 4 個單位
C．向上平移 π 4 個單位	D．向下平移 π 4 個單位

A．y=cos2x,x∈R	B．y=x³+1，x∈R
C．y= e x - e - x 2 ，x∈R	D．y=log₂\|x\|，x∈R且x≠0

A．{0，1，8，9，10}	B．{1，8，9，10}
C．{x\|8≤x≤10}	D．{x\|8≤x≤10或x=1}

A．充分不必要條件	B．必要不充分條件
C．充要條件	D．既不充分也不必要條件

2021-2022學年河南省開封市五縣高一（上）期末數學試卷

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的。

1．下列四組函數中，f（x）與g（x）相等的是（ ）

2．函數f（x）=2lnx+x-6的零點所在區間為（ ）

3．已知命題p：“?x≥0，x2-x+1≥0”，則它的否定為（ ）

4．要得到函數y=2cosx的圖象，只需將函數y=2sin（x+π4）的圖象（ ）

5．若函數y=a-sinx的定義域為R，則實數a的取值范圍為（ ）

6．下列函數中，既是偶函數，又在區間（1，2）內是增函數的為（ ）

7．設a=log23，b=log45，c=2-0.1，則a,b,c的大小關系為（ ）

8．已知x＞0，y＞0，且2x+y=xy,則x+2y的最小值為（ ）

9．已知集合A={x∈N*|1≤x≤10}，集合B={x|x2-9x+8≥0}，則A∩B=（ ）

10．設x∈R，則“-2＜x＜2”是“1＜x＜2”的（ ）

11．若集合A={x|y=x}，B={x|x2-x-2＜0}，則A∩B=（ ）

二、填空題：本題共4小題，每小題5分，共20分。

13．如圖所示，函數f（x）的圖象是折線段ABC，其中A，B，C的坐標分別為（0，4），（2，0），（6，4），則f（f（0））=．（用數字作答）

14．（1）計算：7log76?log65?log54=；（2）已知lg2=a,lg3=b,那么log512=．

15．函數f（x）=2x+5的定義域為 ，值域為 ．

16．記min{x,y,z}表示x,y,z中的最小值，設函數f（x）=min{x,x2-4x+4，-2x+12}，則f（x）的最大值為 ，f（x）≥1的解集為 ．

三、解答題：共70分.解答應寫出文字說明，證明過程或演算步驟。

17．已知函數f（x）=（1-a）x-12，x＜0ax2+2x-a,x≥0．（1）若f（x）在R上單調遞增，求實數a的取值范圍；（2）求f（x）在區間[1，2]上的最大值．

20．求cos105°的值．

21．已知函數f（x），g（x）分別是定義在R上的偶函數和奇函數，且f（x）+g（x）=x2-x+1．（1）求函數f（x）與g（x）的解析式；（2）設函數G（x）=f（x）+a|g（x）+1|，若對任意實數x,G（x）≥32恒成立，求實數a的取值范圍．

1．下列四組函數中，f（x）與g（x）相等的是（　　）

2．函數f（x）=2lnx+x-6的零點所在區間為（　　）

3．已知命題p：“?x≥0，x²-x+1≥0”，則它的否定為（　　）

4．要得到函數y=
2
cosx的圖象，只需將函數y=
2
sin（x+
π
4
）的圖象（　　）

5．若函數y=
a
-
sinx
的定義域為R，則實數a的取值范圍為（　　）

6．下列函數中，既是偶函數，又在區間（1，2）內是增函數的為（　　）

7．設
a
=
lo
g
2
3
，
b
=
lo
g
4
5
，
c
=
2
-
0
.
1
，則a,b,c的大小關系為（　　）

8．已知x＞0，y＞0，且2x+y=xy,則x+2y的最小值為（　　）

9．已知集合A={x∈N^*|1≤x≤10}，集合B={x|x²-9x+8≥0}，則A∩B=（　　）

10．設x∈R，則“-2＜x＜2”是“1＜x＜2”的（　　）

11．若集合
A
=
{
x
|
y
=
x
}
，B={x|x²-x-2＜0}，則A∩B=（　　）

13．如圖所示，函數f（x）的圖象是折線段ABC，其中A，B，C的坐標分別為（0，4），（2，0），（6，4），則f（f（0））=
．（用數字作答）

14．（1）計算：7
lo
g
7
6
?
lo
g
6
5
?
lo
g
5
4
=
；
（2）已知lg2=a,lg3=b,那么log₅12=
．

15．函數f（x）=
2
x
+
5
的定義域為
，值域為
．

16．記min{x,y,z}表示x,y,z中的最小值，設函數f（x）=min{x,x²-4x+4，-2x+12}，則f（x）的最大值為
，f（x）≥1的解集為
．

17．已知函數
f
（
x
）
=
（
1
-
a
）
x
-
1
2
，
x
＜
0
a
x
2
+
2
x
-
a
,
x
≥
0
．
（1）若f（x）在R上單調遞增，求實數a的取值范圍；
（2）求f（x）在區間[1，2]上的最大值．

21．已知函數f（x），g（x）分別是定義在R上的偶函數和奇函數，且f（x）+g（x）=x²-x+1．
（1）求函數f（x）與g（x）的解析式；
（2）設函數G（x）=f（x）+a|g（x）+1|，若對任意實數x,
G
（
x
）
≥
3
2
恒成立，求實數a的取值范圍．