2023-2024學年遼寧省大連市金普新區(qū)九年級（上）期中數學試卷
發(fā)布：2024/10/23 17:0:5
一、選擇題（本題共10小題，每小題2分，共20分，在每個小題給出的四個選項中，只
-
1．下列標志既是軸對稱圖形又是中心對稱圖形的是（ ）
組卷：2874引用：77難度：0.9 -
2．點A（-6，7）關于原點的對稱點的坐標為（ ）
組卷：113引用：2難度：0.7 -
3．一元二次方程2x2-5x+3=0的根的情況為（ ）
組卷：135引用：6難度：0.5 -
4．一元二次方程x2+6x+4=0配方后正確的是（ ）
組卷：398引用：8難度：0.6 -
5．拋物線y=-5（x+2）2-6的頂點坐標是（ ）
組卷：797引用：13難度：0.9 -
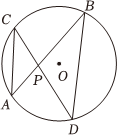6．如圖，⊙O中，弦AB，CD相交于點P，∠A=40°，∠APD=77°，則∠B的大小是（ ）組卷：482引用：2難度：0.7 -
7．將拋物線
先向右平移3個單位，再向上平移2個單位，得到的拋物線是（ ）y=16x2組卷：135引用：1難度：0.5 -
8．“雜交水稻之父”袁隆平和他的團隊探索培育的“海水稻”在某試驗田的產量逐年增加，2018年平均畝產量約500公斤，2020年平均畝產量約800公斤．若設平均畝產量的年平均增長率為x,根據題意，可列方程為（ ）
組卷：1629引用：24難度：0.7
五、解答題（本題共3小題，其中23、24題各11分，25小題12分，共34分）
-
24．問題初探
（1）綜合與實踐數學活動課上，張老師給出了一個問題：如圖1，在△ABC中，AB=AC，∠BAC=90°，點D，E在BC邊上，且∠DAE=45°，則用等式表示線段BD，CE，DE之間的數量關系是 ；
①小明同學經過分析后，將△ABD繞點A逆時針旋轉90°得到△ACF，連接EF，根據三角形全等和勾股定理知識得到線段BD，CE，DE之間的數量關系；
②小強同學經過分析后，將△ABD、△ACE分別沿AD，AE進行翻折，得到△AFD和△AFE，根據三角形全等和勾股定理知識也得到了線段BD，CE，DE之間的數量關系．
請你根據上述兩名同學的分析寫出用等式表示線段BD，CE，DE之間的數量關系是 ；
類比分析
（2）張老師發(fā)現兩名同學分別從旋轉和軸對稱的角度分析、解決問題，張老師將前面問題進行變式，請你解答：如圖4，在△ABC中，AB=AC，∠BAC=90°，點D在BC邊上，點E在BC的延長線上，且∠DAE=45°，用等式表示線段BD，CE，DE之間的數量關系，并證明；
學以致用
（3）如圖5，在四邊形ABCD中，AB=AD，∠BAD=∠BCD=90°，∠EAF=45°，若BC=8，DC=12，CF=6，則BE的長是 ．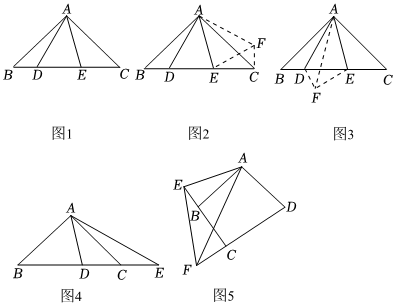
組卷：469引用：1難度：0.1 -
25．問題初探
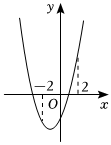
（1）綜合與實踐數學活動課上，張老師給出了一個問題：已知二次函數y=x2+2x-3，當-2≤x≤2時，y的取值范圍為 ；
①小偉同學經過分析后，將原二次函數配方成y=a（x-h）2+k的形式，確定拋物線對稱軸為直線x=h,通過-2、h和2的大小關系，分別確定了最大值和最小值，進而求出y的取值范圍；
②小軍同學畫出如圖的函數圖象，通過觀察圖象確定了y的取值范圍；
請你根據上述兩名同學的分析寫出y的取值范圍是 ；
類比分析
（2）張老師發(fā)現兩名同學分別從“數”和“形”的角度分析、解決問題，為了讓同學們更好的感悟“數形結合”思想，張老師將前面問題變式為下面問題，請你解答：已知二次函數y=x2+2x-3，當a-1≤x≤a+1時，求y的最大值，并寫出a的取值范圍；
學以致用
（3）已知二次函數y=-x2+6x-5，當a≤x≤a+3時，二次函數的最大值為y1，最小值為y2，若y1-y2=3，求a的值．組卷：1138引用：3難度：0.3