2010年新課標七年級數學競賽培訓第30講：創新命題
發布：2024/11/26 3:0:2
一、填空題（共9小題，每小題4分，滿分36分）
-
1．現定義兩種運算：
，對于任意兩個整數a,b,
=a+b-1，
=ab-1，那么
．組卷：48引用：1難度：0.9 -
2．對于任意有理數a,b,c,d,我們規定
，如果abcd=ad-bc，那么x的取值范圍是2x2-1-1＜8．組卷：112引用：5難度：0.9 -
3．餐廳里有兩種餐桌，方桌可坐4人，圓桌可坐9人，若就餐人數剛好坐滿若干張方桌和圓桌，餐廳經理就稱此數為“發財數”，在1～100這100個數中，“發財數”有
個．組卷：99引用：2難度：0.5 -
4．讀一讀：式子“1+2+3+4+5+…+100”表示從1開始的100個連續自然數的和．由于上述式子比較長，書寫也不方便，為了簡便起見，我們可將“1+2+3+4+5+…+100”表示為
，這里“∑”是求和符號．例如：“1+3+5+7+9+…+99”（即從1開始的100以內的連續奇數的和）可表示為100∑n=1n；又如“13+23+33+43+53+63+73+83+93+103”可表示為50∑n=1（2n-1）．同學們，通過對以上材料的閱讀，請解答下列問題：10∑n=1n3
①2+4+6+8+10+…+100（即從2開始的100以內的連續偶數的和）用求和符號可表示為；
②計算：=（填寫最后的計算結果）．5∑n=1（n2-1）組卷：278引用：5難度：0.5 -
5．一個非零自然數若能表示為兩個非零自然數的平方差，則稱這個自然數為“智慧數”，比如16=52-32，故16是一個“智慧數”，在自然數列中，從1開始起，第1990個“智慧數”是
．組卷：160引用：1難度：0.9 -
6．△表示一種運算，它的含義是x△y=
，已知2△1=1xy+1（x+1）（y+A），那么2001△2002的值是．12×1+1（2+1）（1+A）=23組卷：88引用：1難度：0.7 -
7．若規定a△b=
，那么方程3△|x|=4的解x=．a+2b2組卷：126引用：2難度：0.5 -
8．對一切正整數n,有f（n+1）=f（n）+n,且f（1）=1，則f（n）=
．組卷：56引用：1難度：0.7 -
9．將自然數N接寫在每一個自然數的右面（例如，將2接寫在35的右面得352），如果得到的新數都能被N整除，那么N稱為“魔術數”．在小于130的自然數中，魔術數的個數為
．組卷：82引用：2難度：0.5
三、解答題（共12小題，滿分93分）
-
27．沿著圓周放著一些數，如果有依次相連的4個數a,b,c,d滿足不等式（a-d）（b-c）＞0，那么就可以交換b,c的位置，這稱為一次操作．
（1）若圓周上依次放著數1，2，3，4，5，6，問：是否能經過有限次操作后，對圓周上任意依次相連的4個數a,b,c,d,都有（a-d）（b-c）≤0？請說明理由．
（2）若圓周上從小到大按順時針方向依次放著2003個正整數1，2，…，2003，問：是否能經過有限次操作后，對圓周上任意依次相連的4個數a,b,c,d,都有（a-d）（b-c）≤0？請說明理由．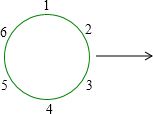
組卷：114引用：4難度：0.5 -
28．假設a#a+b表示經過計算后a的值變為a的原值和b的原值的和，又b#b?c表示經過計算后b的值變為b的原值和c的原值相乘，假設計算開始時a=0，b=1，c=1，對a、b、c同時進行以下計算：
（1）a#a+b；
（2）b#b?c；
（3）c#a+b+c（即c的值變為所得到的a、b的值與c的原值的和）．
連續進行上述運算共三次，試判斷a、b、c三個數值之和是幾位數？組卷：51引用：1難度：0.3