2022-2023學年江西省贛州市興國縣平川中學高一（下）期中數學試卷

一、單選題（每題5分，共40分）

• 1．已知m＞0，則“a＞b”是“am＞bm”的（　　）

  A．充分而不必要條件	B．必要而不充分條件
  C．充分必要條件	D．既不充分也不必要條件
  組卷：201引用：2難度：0.8

  解析

• 2．設i?z=4-3i（i為虛數單位），則復數z的虛部為（　　）

  A．-4

  B．4

  C．-4i

  D．4i
  組卷：109引用：7難度：0.8

  解析

• 3．下列命題正確的是（　　）

  A．有兩個面平行，其余各面都是四邊形的幾何體叫棱柱

  B．有兩個面平行，其余各面都是平行四邊形的幾何體叫棱柱

  C．正六棱錐的側棱和底面邊長一定不相等

  D．棱柱的側面都是全等的平行四邊形
  組卷：92引用：2難度：0.7

  解析

• 4．△ABC的內角A，B，C的對邊分別為a,b,c,若C=

  π

  3

  ，c=

  7

  ，b=3a,則△ABC的面積為（　　）

  A． 3 3 4

  B． 2 - 3 4

  C． 2

  D． 2 + 3 4
  組卷：636引用：10難度：0.9

  解析

• 5．下列說法中正確的是（　　）

  A．若 | a | = | b | ，則 a ， b 的長度相同，方向相同或相反

  B．若向量 a 是向量 b 的相反向量，則 | a | = | b |

  C．若 a ∥ b ，則存在唯一的實數λ使得 a = λ b

  D．在四邊形ABCD中，一定有 AB + AD = AC
  組卷：225引用：2難度：0.8

  解析

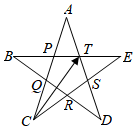• 6．莊嚴美麗的國旗和國徽上的五角星是革命和光明的象征，正五角星是一個非常優美的幾何圖形，且與黃金分割有著密切的聯系．在如圖所示的正五角星中，以A，B，C，D，E為頂點的多邊形為正五邊形，且

  PT

  AP

  =

  5

  -

  1

  2

  ，則（　　）

  A． CT = 3 - 5 2 CA + 3 - 5 2 CE	B． CT = 5 - 1 2 CA + 3 - 5 2 CE
  C． CT = 5 - 1 2 CA + 5 - 1 2 CE	D． CT = 3 - 5 4 CA + 5 - 1 2 CE
  組卷：294引用：8難度：0.6

  解析

• 7．銳角△ABC中，角A、B、C所對邊分別為a、b、c,若b²=a（a+c），則

  3

  sin（B-A）+cosA范圍為（　　）

  A．（ 3 ， 6 + 2 2 ）

  B．（ 6 + 2 2 ，2）

  C．（1，2）

  D．（1， 6 + 2 2 ）
  組卷：269引用：2難度：0.5

  解析

四、解答題（共70分）

• 21．已知向量

  a

  =

  （

  cosx

  ,

  cos

  2

  x

  ）

  ，

  b

  =

  （

  sin

  （

  x

  +

  π

  3

  ）

  ，-

  3

  ）

  ，設函數

  f

  （

  x

  ）

  =

  a

  ?

  b

  +

  3

  4

  ，x∈R．
  （1）求函數f（x）的單調遞增區間；
  （2）當

  x

  ∈

  [

  -

  π

  6

  ，

  π

  3

  ]

  時，方程

  2

  f

  （

  x

  +

  π

  4

  ）

  =

  1

  2

  m

  -

  1

  有兩個不等的實根，求m的取值范圍；
  （3）若函數

  g

  （

  x

  ）

  =

  f

  （

  x

  -

  π

  12

  ）

  ，對任意的

  x

  1

  ∈

  [

  0

  ，

  π

  2

  ]

  ，存在

  x

  2

  ∈

  [

  0

  ，

  π

  2

  ]

  ，使得f（x₁）+kg（x₂）＞0，求實數k的取值范圍．
  組卷：68引用：2難度：0.5

  解析

• 22．將二次函數y=x²的圖象在坐標系內自由平移，且始終過定點P（t,t²），則圖象頂點A也隨之移動，設頂點A（x,y）所滿足的表達式為二次函數y=f（x）．例如，當t=1時，f（x）=-x²+2x；當t=2時，f（x）=-x²+4x.
  （1）當t=2，圖象平移到某一位置時，且P與A不重合，有

  OP

  ⊥

  PA

  ，其中O為坐標原點，求

  PA

  的坐標；
  （2）記函數g（x）=f（x）-2x+1在區間[2，4]上的最大值為M（t），求M（t）的表達式；
  （3）對于常數λ（λ＞0），若無論圖象如何平移，當A，P不重合時，總能在圖象上找到兩點B，C，使得

  BC

  =

  λ

  PA

  ，且直線BC與f（x）無交點，求λ的取值范圍．
  組卷：17引用：2難度：0.6

  解析